一、引言
相关性分析提供了一种简单而直观的方法来初步筛选特征。通过计算特征与目标变量之间的相关系数,我们能够快速地评估各个特征与预测目标之间的线性关系强度。
在统计学中,最常用的相关系数有两种:皮尔逊相关系数(Pearson correlation coefficient)和斯皮尔曼等级相关系数(Spearman’s rank correlation coefficient)。皮尔逊相关系数用于衡量两个连续变量之间的线性相关程度,而斯皮尔曼相关系数则适用于评估两个变量的等级间的单调相关关系,特别适用于非线性关系的数据。
应用注意事项:
- 相关性分析只能捕捉到线性关系或单调关系,对于复杂的非线性关系可能无法有效识别。
- 高相关性并不意味着因果关系,有时候两个特征之间的高相关性可能只是因为它们共同受到第三个因素的影响。
二、实现过程
2.1 准备数据
data = pd.read_csv(r'dataset.csv')df = pd.DataFrame(data)
2.2 目标变量和特征变量
target = 'target'features = df.columns.drop(target)
特征变量如下:
2.3 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(df[features].values, df[target].values, test_size=0.2, random_state=0)2.4 重构训练集数据
进行训练集数据重构:
train_X = pd.DataFrame(X_train, columns=features)train_y = pd.DataFrame(y_train, columns=[target])train = pd.concat([train_X, train_y],axis = 1)print(train)
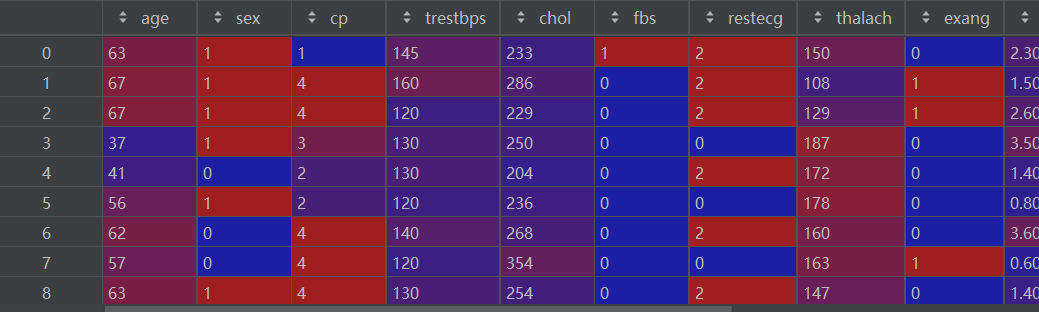
打印结果:
2.5 相关性分析并可视化
代码:
sns.set(font_scale=1.2)plt.rc('font',family=['SimSun'], size=12)plt.figure(figsize=(10, 8))plt.subplots_adjust()ax = sns.heatmap(train.corr(), annot=True, xticklabels=False, fmt=".2f")ax.set_title('相关性热力图') # 图标题plt.xticks(rotation=45)plt.tight_layout()plt.show()
结果:
计算了这些属性之间的相关系数,并通过热力图的方式进行了可视化。通过热力图,我们可以直观地看到各属性与标签之间的相关性如何。
原创文章,作者:guozi,如若转载,请注明出处:https://www.sudun.com/ask/90411.html