原文:jax.readthedocs.io/en/latest/
JAX 增强提案(JEPs)
原文:jax.readthedocs.io/en/latest/jep/index.html
大多数更改可以通过简单的问题/讨论和拉取请求来讨论。
但是,某些更改范围更广或需要更多讨论,应作为JEP 实施。这允许您创建可以在拉取请求中讨论的长文档。
JEP 的结构最初尽可能保持轻量级,以后可能会进行扩展。
当你需要使用一个 JEP 时
如果您的更改需要设计文档。我们更喜欢将设计收集为JEP,以便更好地发现和进一步参考。
如果改变需要广泛讨论。关于问题和拉取请求的相对较短的讨论是可以接受的,但较长的讨论对于后续的消化来说是不切实际的。 JEP 允许您通过更新主文档来添加讨论摘要,并且可以在添加JEP 的拉取请求中讨论更新本身。
如何开始一个 JEP
首先,使用JEP 标签创建一个问题。所有与JEP 相关的拉取请求(即JEP 本身的添加和实现拉取请求)都必须链接到此问题。
接下来,创建一个拉取请求以添加名为%d-{short-title}.md 的文件。这里的数字是发行号。
263: JAX PRNG设计
2026: JAX 可翻译函数的自定义JVP/VJP 规则
4008: 自定义VJP 和nodiff_argnums 更新
4410: 全方位
9263: 型密钥和可插拔RNG 设计
9407: JAX 类型改进语义设计
9419: Jax 和Jaxlib 版本控制
10657: JAX 中的顺序副作用
11830: jax.remat/jax.checkpoint 的新实现
12049: JAX 类型注释路线图
14273: shard_map (shmap) 用于简单的每设备代码
15856: jax.extend,扩展模块
17111: shard_map(和其他map)的高效转置
18137: JAX NumPy 和SciPy 包装范围
一些早期的JEP 实际上是后来从其他文档、问题或拉取请求转换而来的,因此它们可能不完全遵循上述过程。
JAX PRNG 设计
原文:jax.readthedocs.io/en/latest/jep/263-prng.html
需要PRNG 设计
它易于使用且富有表现力,因为它不限制用户编写精确执行所需行为的数值程序的能力。
以独立于后端的方式实现可重复的程序执行。
@jit 具有跨编译边界和设备后端不变的语义,
使用启用矢量化的SIMD 硬件生成数组值,
它是可并行的,因为它不会在随机函数调用之间不存在数据依赖性的情况下添加排序约束。
可扩展到多个副本、多核和分布式计算。
与JAX 和XLA 语义和设计理念(最终由其他实际问题驱动的理念)保持一致。
因此,我们认为设计应该具有功能性。另一个推论是在软件中执行PRNG,至少在当前的硬件限制内。
TLDR JAX PRNG=Threefry 计数器PRNG + 面向函数数组的分区模型
内容
三种编程模型和玩具示例程序
设计
更真实的用户示例程序
权衡和替代方案
三种编程模型和玩具示例程序
下面是一个类似于Numpy 程序中常用的有状态全局PRNG 的玩具示例。
def foo(): 返回bar() + baz()
def bar(): 返回rand(RNG, (3, 4))
def baz(): 返回rand(RNG, (3, 4))
def main():
全球RNG
RNG=随机状态(0)
返回foo()
为了在这里实现可重复性,您需要控制bar() 和baz() 的计算顺序,即使它们之间没有显式的数据依赖关系。这种由可重复性(#2) 产生的排序要求违反了并行性(#5),并且与JAX 或XLA (#6) 的函数语义不一致,在JAX 或XLA (#6) 中,子表达式可以按任何顺序求值。即使您不需要可重复性并且可以按任何顺序进行评估,调用之间的并行化(#5) 仍然很困难,因为共享状态需要更新。此外,该模型要求Python 和编译后的代码访问并维护相同的PRNG 状态,以实现编译不变性(#3) 和扩展到多个副本(#6),这可能会带来工程挑战。最后,foo() 无法在不影响其自身(隐式)PRNG 状态的情况下调用bar() 或baz(),因此表达能力受到限制(#1)。
模型是否支持矢量化(#4)取决于一些额外的细节。在Numpy 中,PRNG 向量化受到顺序相等保证的约束。
[1]: 与rng=np.random.RandomState(0)
[2] rng.randn(2) 中的:
输出[2]:数组([1.76405235,0.40015721])
[3]: 与rng=np.random.RandomState(0)
[4]: np.stack([rng.randn() for _ in range(2)])
输出[4]:数组([1.76405235,0.40015721])
我们通过允许在生成数组的原始PRNG 函数调用中进行向量化(#4)来放弃这种顺序相等保证(例如,使用形状参数调用rand())。尽管本节中描述的三种编程模型中的任何一种都可以支持这种向量化,但我们还是有动力遵循下一节中描述的基于计数器的PRNG 实现。
有状态PRNG 用户编程模型的前景黯淡。下面是特征模型的示例,但它缺少一个称为分段的重要元素。
def foo(rng_1):
y,rng_2=baz(rng_1)
z, rng_3=条(rng_2)
返回y + z,rng_3
def bar(x, rng):
val, new_rng=rand(rng, (3, 4))
返回值,new_rng
def baz(x, rng):
val, new_rng=rand(rng, (3, 4))
返回值,new_rng
def main():
foo(随机状态(0))
该模型通过生成随机值的所有函数(原始或非原始)显式地将PRNG 状态线程化。也就是说,所有随机函数都必须接受并返回状态。对于foo(),对baz() 的调用和对bar() 的调用之间存在显式数据依赖关系,因此与以前的模型不同,数据流(因此顺序)是显式的,并且JAX 与现有模型一致(#7) 的语义。这种显式线程在编译边界之前不会更改语义(#3)。
对于程序员来说,显式线程很不方便。但更糟糕的是,它实际上并没有提高表达能力(#1): foo() 在调用bar() 或baz() 期间仍然无法维持自己的PRNG 状态。在不知道调用者或被调用的子例程的情况下,该函数必须防御性地通过并在各处返回rng 状态。此外,即使顺序在函数式编程意义上明确表达,一切仍然是顺序的,这改善了并行化的前景(#5)和扩展到多个副本的能力(#6)。
换句话说,显式地线程化状态并使代码工作并不能实现表达性目标(#1)和性能目标(#5、#6)。
前两个模型的主要问题是它们有太多的顺序依赖性。我们使用功能上可拆分的PRNG 来减少顺序依赖性。拆分是一种将新的PRNG 状态“分叉”为两个PRNG 状态的机制,同时保留通常所需的PRNG 属性(两个新流可以在计算上并行化并可以生成独立的随机值)(即与多流类似)。
def foo(rng_1):
rng_2, rng_3=分割(rng_1, 2)
返回条(rng_2) + 嗡嗡声(rng_3)
def bar(x, rng):
返回rand(rng, (3, 4))
def baz(x, rng):
返回rand(rng, (3, 4))
def main():
foo(随机状态(0))
注意事项:
bar() 和baz() 的调用顺序并不重要。可以按任何顺序对它们进行评估,而不会影响结果值。这解决了剩余的性能目标(#5、#6)。
它比其他函数模型(#1)更具表现力,因为该函数不需要返回PRNG 的更新版本,并且可以直接调用随机子例程,而不会影响现有的PRNG 状态。
尽管图中未显示,但由于选择(2),推进PRNG 状态的唯一方法是调用split()。因此,有两种方法可以实现(1):要么在用户程序中添加对split() 的显式调用,如上例所示,要么添加显式线程。具体细节有所不同。我们推荐前者的显式分割版本。因为你可以基于此轻松实现显式线程版本。
设计
您可以使用基于计数器的PRNG 设计,尤其是并行随机数: 中描述的Threefry 哈希函数,就像1、2、3 一样简单。利用计数器实现高效的矢量化。您可以通过将整数范围[k + 1, …, k + sample_size] 中的哈希函数映射到给定键来以向量化方式生成值数组。使用密钥和哈希函数实现可分割的PRNG。换句话说,拆分是一种从现有密钥生成两个新密钥的方法。
类型示例=Int256
type Key=Sample — 拆分的密钥标识
类型计数=Int32
Hash : Key – Count – Int256 — 输出类型等于Key 和Sample
分体式: 钥匙- (钥匙、钥匙)
分割键=(哈希键0, 哈希键1)
draw_samples : 键- Int – [示例]
draw_samples key n=map(哈希键)[1.n]
令人惊讶的是,采样与分割非常相似。重要的是输出类型的差异(即使类型被认为是相同的)。在某些情况下,这些值用于形成感兴趣的随机样本(例如,将随机位转换为表示随机正态分布的Float)。而在其他情况下,该值用作进一步散列的键。
哈希函数参数(即Key 和Count 类型)不对称。后者只是简单地增加一个整数值,因此可以通过对任意数字的计算轻松地推进它,而前者只能通过散列来推进。因此,矢量化使用计数参数。
更现实的示例用户程序
如果某个步骤需要PRNG(例如dropout 或VAE 训练),则主机上的训练循环如下所示:
rng=lax.rng.new_rng()
对于我在xrange(num_steps):
rng, rng_input=lax.rng.split(rng)
params=Compiled_update(rng_input, params, 下一个(batch))
请注意,虽然显式拆分随机数生成器给用户带来了负担,但代码根本不需要返回随机数生成器。
在这里,我们展示了如何使用stax 神经网络构建器库中的PRNG 模型来实现dropout。
def dropout(rate, mode=\’train\’):
def init_fun(input_shape):
返回输入形状,()
def apply_fun(rng, 参数, 输入):
如果模式==\’火车\’:
keep=lax.random.bernoulli(rng, 速率, 输入.shape)
返回np.where(保留, 输入/速率, 0)
: 其他
返回输入
返回init_fun、apply_fun
这里的rng值只是一个用于散列的key,并不是一个特殊的对象。 rng 参数传递给每个apply_fun,并且必须由串行和并行组合器进行处理以进行拆分。
def 序列号(*层):
init_funs, apply_funs=zip(*层)
def init_fun(input_shape):
.
def apply_fun(rng, 参数, 输入):
rngs=split(rng, len(层))
对于zip 中的rng、param、apply_fun (rngs、params、apply_funs):
输入=apply_fun(rng, 参数, 输入)
返回输入
返回init_fun、apply_fun
def 平行(*层):
init_funs, apply_funs=zip(*层)
def init_fun(input_shape):
.
def apply_fun(rng, 参数, 输入):
rngs=split(rng, len(层))
返回[f(r, p, x) for f, r, p, x in zip(apply_funs, rgs, params, input)]
返回init_fun、apply_fun
我们将使用一个简单的Split 扩展版本,它可以生成多个副本。
折衷和替代方案
没有使用设备硬件PRNG。
目前无法控制所有后端的硬件PRNG状态。
即使您可以这样做,它也取决于后端,因此您可能需要在随机调用之间引入顺序依赖关系,以确保确定性排序,从而确保可重复性。
我们没有发现软件PRNG 成为瓶颈的任何工作负载。
您可以考虑提供额外的API,允许访问硬件PRNG,以便用户可以放弃其他期望(例如严格的再现性)。
我们已经放弃了顺序等效的保证。换句话说,在一次调用中创建随机数组会产生与一一创建展平数组的随机元素相同的值。
此属性可能与矢量化不兼容(高优先级)。
我不知道哪些用户或样本认为这个属性很重要。
用户可以在此API 之上创建层来提供这种保证。
不可能完全遵循numpy.random API。
为 JAX-可变换函数定义自定义 JVP/VJP 规则
原文:jax.readthedocs.io/en/latest/jep/2026-custom-derivatives.html
这是一个设计文档,描述了jax.custom_jvp 和jax.custom_vjp 的设计和实现背后的一些想法。有关用户文档,请参阅教程笔记本。
在JAX 中定义微分规则有两种方法。
使用jax.custom_jvp 和jax.custom_vjp 为已可JAX 翻译的Python 函数定义自定义区分规则。
定义一个新的core.Primitive 实例及其所有转换规则,包括从其他系统(例如求解器、模拟器和通用数值系统)调用函数。
本文将仅介绍#1。
内容
目标
不适用
主要问题描述
vmap-removes-custom-jvp 的语义问题
Python灵活性问题
解决思路
实施说明
目标
我们希望允许用户自定义其代码的正向和/或反向模式差分行为。这种定制
它应该显示清晰且一致的语义以及它如何与其他JAX 转换结合使用。
它应该足够灵活,能够支持Autograd 和PyTorch 中的用例和工作流程,例如使用Python 控制流的微分和NaN 调试工作流程。
作为一名JAX 开发人员,我希望创建logit 和exit 等库函数,这些函数定义在其他原语之上,但具有类似原语的行为以用于区分目的。因此,我想为它们定义自定义区分规则。这些规则可能更加稳定。或者更有效率。特别是,我不想为logit 或exit 等函数指定vmap 或jit 规则。
作为扩展目标,我们希望创建一个适合高级用户的JAX 环境,这些用户想要为固定点、odeint 等高阶函数添加自定义微分规则,但本设计文档并没有解决这个问题。我们希望避免消除这个问题的良好解决方案。
所以我们的主要目标是
解决了vmap-removes-custom-jvp 语义(#1249) 和
允许在自定义VJP 中使用Python(例如用于调试NaN)。
次要目标是3. 清理并简化用户体验(符号零、kwargs 等) 4. 迈向用户可以轻松添加fix_point、odeint、root 等的世界。
总的来说,我们希望关闭#116、#1097、#1249、#1275、#1366、#1723、#1670、#1875、#1938 并替换#636、#818 和其他问题的Custom_transforms 机制。
非目标
以下是我们不打算实现的目标:
custom_transforms 机制旨在为转换提供通用机制来自定义其行为,原则上(尽管实际上并非如此)允许用户以某种方式修改其他转换的“透明”行为。允许您自定义任何转换的规则。同时继承.相反,它仅旨在解决三角洲(分别是JVP 和VJP)中的定制问题。 实际上,唯一需要的用例是差异化,专门从事差异化可以降低复杂性并提高灵活性。为了控制所有规则,用户可以直接创建原始函数。
我们并不打算将数学之美置于用户便利性、实现简单性和清晰度之上。特别是,自定义VJP 签名a – (b, CT b –o CT a) 虽然在数学上很漂亮,但由于返回类型闭包而很难用Python 机制实现。处理步骤残差的显式方法。
序列化支持,即加载分阶段序列化程序表示并执行评估以及其他JAX 转换,目前超出了这些自定义JVP/VJP 转换规则的范围。序列化不仅对于想要保留计算表示(并在加载后对其进行转换)的研究人员有用,而且还可以考虑在Python 之外实现jaxprs 转换,或者作为MLIR 语言的一部分。通过将此定义为本设计的非目标,对Python 可调用项的放置位置的限制更少。
主要问题描述
vmap 移除自定义 JVP 语义问题
自定义JVP 语义中vmap 删除的问题在于,custom_transforms 规则的功能微分和vmap 的组合错误。
# 旧的custom_transforms API 被替换
@jax.custom_transforms
定义f(x):
返回2。 *X
# f_vjp : a – (b, CT b –o CT a)
def f_vjp(x):
返回f(x), lambda g: 3. * x # 3 而不是2
jax.defvjp_all(f, f_vjp)
毕业(f)(1.)#3。
vmap(grad(f))(np.ones(4)) # [3. 3. 3. 3.]
grad(lambda x: vmap(f)(x).sum())(np.ones(4)) # [2. 2. 2. 2.]
grad-of-vmap 的最后一行给出了意想不到的结果。通常,当您应用vmap 或非导数转换时,会删除自定义微分规则。 (如果定义了自定义VJP 规则,则应用jvp 将导致错误。)
问题在于,转换的行为就像重写,而vmap 转换有效地重写了函数,使其不再调用自定义规则中新引入的原语(因此grad 实际上不再为自定义规则生成结果)。更具体地说,custom_transforms 机制为要在f(x) 求值中应用的函数设置环境。
{ 拉姆达;
设b=f_primitive a
[b]}
这里,f_primitive 是与自定义VJP 规则关联的新原语(为每个custom_transforms 函数引入,实际上是为每个函数调用引入)。当计算grad(f)(x) 时,微分机制遇到f_primitive 并使用自定义规则对其进行处理。
然而,由于f_primitive 对vmap 是透明的,即vmap 对f_primitive 的(有效内联)定义进行操作,因此函数vmap(f) 实际上是
{ 拉姆达;
设b= 2 。
[b]}
换句话说,vmap通过重写基本原语及其变换规则所表示的函数,完全删除了f_primitive。
更一般地, vmap(f) 的语义被定义为对f 的调用,因此删除自定义派生规则将导致语义不一致。换句话说,由于我们将其定义如下,
vmap(f)(xs)==np.stack([f(x) for x in xs])
我们必须有
jvp(vmap(f))(xs)==jvp(lambda xs: np.stack([f(x) for x in xs]))
但是,如果f 具有自定义导数规则,则此属性不再可用,因为自定义导数规则仅在右侧版本中使用,而在左侧版本中不使用。
这个问题不仅限于vmap,还适用于任何将函数f 变换的语义定义为调用函数f 而不是将其重写为单独函数的变换。蒙版变换也属于这一类。各种微分变换和所有一元函数都会产生余弦变换的假设不属于此类。
(其他自定义规则(例如自定义vmap 规则)之间的交互可能更加复杂,这表明custom_transforms 问题的框架过于宽泛。)
Python 的灵活性问题
在JAX 中,与Autograd 和PyTorch 一样,但与TF1 不同,Python 函数的微分是在执行和跟踪函数时执行的。用户喜欢这种行为的原因有很多。
首先也是最重要的是,它支持基于pdb 的工作流程,例如检查数字和捕获NaN。 这意味着用户可以使用标准Python 调试器和其他Python 本机工具进行调试。
的代码,甚至可以检查运行时值以理解示例中的数值行为,并捕获诸如 NaN 等基本的运行时错误。事实上,就在为这一设计相应的 PR 工作时,特别是在 odeint 原语上,我多次使用运行时值检查来调试问题,增强了我对这一在 Python 中的关键用户工作流程的信心。一个特别方便的技巧是,在自定义 VJP 规则中插入调试器断点,以在向后传递中的特定点进入调试器。
其次,它允许对 Python 原生控制流进行微分。 我们不确定在最终的软件成品中实际使用这种功能的频率,但当用户首次尝试 JAX 或 Autograd 时,他们通常会对这种自由感到印象深刻。我们在 JAX 和 Autograd 的 README、幻灯片演示和演示中包含它是有原因的。放弃这种能力将是从 Autograd 后退的一步。我们希望 JAX 拥有最好的自动微分能力。
然而,custom_transforms 机制并没有提供这种 Python 支持的灵活性。也就是说,因为它是根据来自用户函数和自定义微分规则的 Python 代码的 jaxpr 形成而实现的,这样的代码会导致抽象值追踪错误:
# old custom_transforms api to be replaced
@jax.custom_transforms
def f(x):
if x > 0:
return x
else:
return 0.
def f_vjp(x):
return …
jax.defvjp_all(f, f_vjp)
grad(f)(1.) # Error!
解决方案思路
dougalm@ 已经通过 core.call 解决了这些问题的主要思想。也就是说,我们可以将为用户函数指定自定义 JVP 规则的任务框定为一个新的 Python 级别调用原语(不会添加到 jaxpr 语言中;详见下文)。这个新的调用原语与 core.call 类似,有一个关联的用户 Python 函数,但额外还有一个表示 JVP 规则的第二个 Python 可调用对象。让我们称这个新的调用原语为 custom_jvp_call。
类似于 vmap 如何通过应用于要调用的函数来与 core.call 交互一样,变通地写成原语的柯里化版本,vmap 与 custom_jvp_call 交互,它们有效地穿过它并应用于底层的 Python 可调用对象。这种行为意味着我们已经解决了 vmap 移除自定义 JVP 语义的问题。
vmap(call(f)) == call(vmap(f))
对于新的原语 custom_jvp_call,我们简单地对它涉及的两个函数应用 vmap:
vmap(custom_jvp_call(f, f_jvp)) == custom_jvp_call(vmap(f), vmap(f_jvp))
这种行为意味着我们已经解决了 vmap-移除-custom-jvp 语义问题。
jvp 变换的交互方式如人所预期的那样:它只是调用 f_jvp,
jvp(call(f)) == call(jvp(f))
jvp(custom_jvp_call(f, f_jvp)) == f_jvp
因为custom_jvp_call类似于core.call(而不是像xla.xla_call那样),它不会提升其输入的抽象级别(因为它不延迟任何内容或将任何内容转出),这意味着我们解决了 Python 灵活性问题:用户 Python 函数没有约束(除了jvp或vjp所需的常规函数编程约束)。
评估和编译怎么办?这两种方式是“退出”JAX 系统的两种方式,因为在这些步骤之后不能再应用额外的转换。因此,它们的规则是微不足道的:
eval(call(f)) == eval(f)
jit(call(f)) == hlo_call(jit(f))
eval(custom_jvp_call(f, f_jvp)) == eval(f)
jit(custom_jvp_call(f, f_jvp)) == hlo_call(jit(f))
换言之,如果一个 JVP 规则在将custom_jvp_call(f, f_jvp)重写为f_jvp之前没有重写,那么当我们到达评估点eval或用jit转出至 XLA 时,微分永远不会被应用,因此我们只需忽略f_jvp并且像core.call一样行事。然而,由于下面讨论的问题,custom_jvp_call的部分评估规则必须更加复杂,因为部分评估不仅仅用于用jit转出至 XLA。
“初始样式”jaxpr 形成原语的唯一剩余问题与lax.scan等有关,并且它们的转换规则也有所不同。这些原语代表了一种不同类型的“转出至 jaxpr”,与编译不同,因为我们可以在转出的 jaxpr 上执行额外的转换。也就是说,当lax.scan形成一个 jaxpr 时,它并没有退出转换系统,因为当我们对lax.scan应用 jvp 或 vmap 时,需要对 jaxpr 所代表的函数应用它。
另一种表述剩余问题的方式是,像lax.scan这样的初始样式原语依赖于能够往返到一个 jaxpr 并返回到 Python 可调用对象的能力,同时保留语义。这必须意味着也要保留自定义微分规则的语义。
解决方案是使用一点动态作用域:当我们将一个初始样式原语转出至 jaxpr 时,例如在 lax_control_flow.py 中的原语,我们在全局跟踪状态上设置一个位。当该位被设置时,我们使用一个初始样式custom_jvp_call_jaxpr原语,而不是使用最终样式的custom_jvp_call原语,并且提前跟踪函数f和f_jvp到 jaxpr,以使初始样式处理更容易。custom_jvp_call_jaxpr原语在其他方面与最终样式版本类似。
(脚注:道德上,我们在绑定custom_jvp_call_jaxpr之前为f和f_jvp都形成 jaxpr,但是我们需要延迟f_jvp的 jaxpr 形成,因为它可能调用自定义 JVP 函数,因此急速处理将导致无限递归。我们在一个 thunk 中延迟该 jaxpr 形成。)
如果我们放弃 Python 的灵活性问题,我们可以仅仅使用custom_jvp_call_jaxpr,而不需要单独的 Python 级原语custom_jvp_call。
API
a -> b函数的自定义 JVP 由(a, Ta) -> (b, T b)函数指定:
# f :: a -> b
@jax.custom_jvp
def f(x):
return np.sin(x)
# f_jvp :: (a, T a) -> (b, T b)
def f_jvp(primals, tangents):
x, = primals
t, = tangents
return f(x), np.cos(x) * t
f.defjvp(f_jvp)
(有趣的自动微分说明:为了使规则适用于高阶微分,必须在 f_jvp 的主体中调用 f;这排除了 f 内部和切线计算之间某些工作共享的类型。)
一个 a -> b 函数的自定义 VJP 是通过一个 a -> (b, c) 前向传递函数与一个 (c, CT b) -> CT a 反向传递函数指定的:
# f :: a -> b
@jax.custom_vjp
def f(x):
return np.sin(x)
# f_fwd :: a -> (b, c)
def f_fwd(x):
return f(x), np.cos(x)
# f_bwd :: (c, CT b) -> CT a
def f_bwd(cos_x, g):
return (cos_x * g,)
f.defvjp(f_fwd, f_bwd)
签名 a -> (b, CT b –o CT a) 更具美感,但支持它将使实现变得更复杂,可能需要妥协表达性的愿望。 Python 可调用对象之所以是不透明的(除非我们追踪它们到 jaxpr 并且迫切地执行,这会放置表达约束),在这种情况下,我们可能会返回一个具有 vmap 追踪器的可调用对象,我们需要在正向传递期间了解它们。
我们可以添加方便的包装器,例如一次为单个参数定义 JVP 规则(就像我们在原语内部做的那样)。 但因为这个提案本身已经足够复杂,我决定不使用方便的层;现在让我们保持最小的东西。
API 还有一些其他的花哨功能:
输入和输出类型 a、b 和 c 可以是 jaxtypes 的任意 pytrees。
当可以使用 inspect 模块将参数按名称(关键字参数)解析为位置时,支持这种方式。 这是对 Python 3 改进的实验性质能力以编程方式检查参数签名的一部分。 我认为这是正确的,但不完整,这是一个很好的状态。(另见 #2069。)
可以使用 nondiff_argnums 标记参数为非可区分的,并且与 jit 的 static_argnums 一样,这些参数不必是 JAX 类型。 我们需要设置一种约定来传递这些参数给规则。 对于具有类型签名 (d, a) -> b 的原始函数,其中 d 表示不可区分的类型,JVP 规则的签名是 (a, T a, d) -> T b,VJP 规则的反向组件签名是 (d, c, CT b) -> CT a。 也就是说,在自定义 JVP 规则中,非可区分的参数在 primals 和 tangents 之后按顺序传递,并且在自定义 VJP 规则的反向函数中的残差之前按顺序传递。
实现注意事项
更新了 jax.experimental.odeint
由于 odeint 是一个相当复杂的自定义 VJP 规则的用户,除了只更新它以使其能够正常工作外,我还希望将其修改为新的自定义 VJP API 的规范用户,以此来测试该 API 是否良好。
在此过程中,我对 odeint 实现进行了其他改进:
删除了解开/重新解开的样板代码
利用 lax.scan 来消除索引更新逻辑
在简单的单摆基准测试中加速了 20+%。
对每个变换添加了自定义绑定方法,用于自定义导数调用原语 custom_jvp_call 和 custom_vjp_call。 这类似于 core.call_bind,但我们不处理 env traces:这些只是错误。
添加了custom_lin原语,它在使用自定义 VJP 规则时被分阶段转化为线性 jaxprs 以进行转置。
由于我们的反向模式自动微分分解为线性化、部分求值和转置,我们的自定义 VJP 规则在两个独立步骤中处理:一个在线性化期间,另一个在转置期间。
线性化步骤,即custom_vjp_call的 JVP 规则,将custom_lin应用于切线值;custom_lin携带用户的自定义反向传播函数,并且作为一个原语,它只有一个转置规则。
这一机制在#636中有更详细的描述。
为了防止
自定义 _vjp 和 nondiff_argnums 更新指南
原文:jax.readthedocs.io/en/latest/jep/4008-custom-vjp-update.html
mattjj@ Oct 14 2020
本文假设您熟悉 jax.custom_vjp,如用于 JAX 可转换 Python 函数的自定义导数规则笔记本中所述。
更新内容
在 JAX 的PR #4008之后,传递给 custom_vjp 函数的 nondiff_argnums 的参数不能是 Tracers(或 Tracer 的容器),这基本上意味着为了允许任意可转换的代码,nondiff_argnums 不应该用于数组值的参数。相反,nondiff_argnums 应该仅用于非数组值,如 Python 可调用对象或形状元组或字符串。
无论我们以前用 nondiff_argnums 用于数组值的地方,我们应该将它们作为常规参数传递。在 bwd 规则中,我们需要为它们生成值,但我们可以只生成 None 值来指示没有相应的梯度值。
例如,这是编写 clip_gradient 的旧方法,当 hi 和/或 lo 是来自某些 JAX 转换的 Tracer 时将无法工作。
from functools import partial
import jax
@partial(jax.custom_vjp, nondiff_argnums=(0, 1))
def clip_gradient(lo, hi, x):
return x # identity function
def clip_gradient_fwd(lo, hi, x):
return x, None # no residual values to save
def clip_gradient_bwd(lo, hi, _, g):
return (jnp.clip(g, lo, hi),)
clip_gradient.defvjp(clip_gradient_fwd, clip_gradient_bwd)
这里是新的,令人惊叹的方法,支持任意转换:
import jax
@jax.custom_vjp # no nondiff_argnums!
def clip_gradient(lo, hi, x):
return x # identity function
def clip_gradient_fwd(lo, hi, x):
return x, (lo, hi) # save lo and hi values as residuals
def clip_gradient_bwd(res, g):
lo, hi = res
return (None, None, jnp.clip(g, lo, hi)) # return None for lo and hi
clip_gradient.defvjp(clip_gradient_fwd, clip_gradient_bwd)
如果您使用旧方式而不是新方式,在可能出错的任何情况下(即将 Tracer 传递给 nondiff_argnums 参数时),您将会收到一个大声的错误。
这是一个我们实际上需要使用 custom_vjp 的情况,与 nondiff_argnums:
from functools import partial
import jax
@partial(jax.custom_vjp, nondiff_argnums=(0,))
def skip_app(f, x):
return f(x)
def skip_app_fwd(f, x):
return skip_app(f, x), None
def skip_app_bwd(f, _, g):
return (g,)
skip_app.defvjp(skip_app_fwd, skip_app_bwd)
解释
将 Tracers 传递到 nondiff_argnums 参数中一直是有 bug 的。虽然有些情况下工作正常,但其他情况会导致复杂和令人困惑的错误消息。
这个 bug 的本质在于 nondiff_argnums 的实现方式很像词法闭包。但是那时候,对于Tracers 的词法闭包并不打算与custom_jvp/custom_vjp一起工作。以这种方式实现 nondiff_argnums 是一个错误!
PR #4008 修复了所有与 custom_jvp 和 custom_vjp 相关的词法闭包问题。 哇哦!也就是说,现在 custom_jvp 和 custom_vjp 函数和规则可以对 Tracers 进行词法闭包了。对于所有非自动微分转换,一切都会顺利进行。对于自动微分转换,我们将得到一个清晰的错误消息,说明为什么我们不能针对 custom_jvp 或 custom_vjp 关闭的值进行微分:
检测到对于一个闭包值的自定义 _jvp 函数的微分。这不被支持,因为自定义 JVP 规则仅指定如何针对显式输入参数微分自定义 _jvp 函数。
尝试将闭包值传递给 custom_jvp 函数作为参数,并调整 custom_jvp 规则。
通过这种方式加强和健壮custom_jvp和custom_vjp时,我们发现允许custom_vjp在其nondiff_argnums中接受Tracer将需要大量的簿记工作:我们需要重写用户的fwd函数以返回这些值作为残差,并重写用户的bwd函数以接受它们作为普通残差(而不是像在nondiff_argnums中那样接受它们作为特殊的前导参数)。这似乎可能是可管理的,直到你考虑我们如何处理任意的 pytrees!此外,这种复杂性并非必要:如果用户代码将类似数组的不可区分参数视为常规参数和残差处理,一切都已经可以正常工作。(在 #4039 之前,JAX 可能会抱怨涉及整数值输入和输出的自动微分,但在 #4039 之后,这些问题将会解决!)
与custom_vjp不同,将custom_jvp与nondiff_argnums参数(即Tracer)一起使用是很容易的。因此,这些更新只需要在custom_vjp中进行。
全面暂存
原文:jax.readthedocs.io/en/latest/jep/4410-omnistaging.html
mattjj@ Sept 25 2020
这更像是升级指南而不是设计文档。
目录
简而言之
“全面暂存”是什么以及其有何用处?
开启全面暂存可能导致哪些问题?
使用 jax.numpy 进行形状计算
副作用
基于 XLA 优化的小数值差异
依赖于已更改的 JAX 内部 API
触发 XLA 编译时错误
简而言之
发生了什么?
JAX 的跟踪基础设施发生的名为“全面暂存”(google/jax#3370)在 jax==0.2.0 中启用。此更改改善了内存性能、跟踪执行时间并简化了 jax 内部,但可能导致某些现有代码出现问题。通常情况下,问题是由于有 bug 的代码引起的,因此从长远来看最好修复这些 bug,但全面暂存也可以作为临时解决方法禁用。我们乐意帮助您进行修复!
如何知道全面暂存破坏了我的代码?
判断全面暂存是否负责的最简单方法是禁用全面暂存并查看问题是否消失。请参阅下面的“开启全面暂存可能导致哪些问题?”部分。
如何暂时禁用全面暂存?
注意:这适用于 JAX 版本 0.2.0 到 0.2.11;在 JAX 版本 0.2.12 及更高版本中无法禁用全面暂存
暂时可以通过以下方式禁用全面暂存
将 shell 环境变量 JAX_OMNISTAGING 设置为 falsey;
如果你的代码使用 absl 解析标志,则将布尔标志 jax_omnistaging 设置为 falsey;
在主文件顶部附近使用此语句:
jax.config.disable_omnistaging()
如何修复全面暂存暴露的错误?
全面暂存最常见的问题远远超过了使用 jax.numpy 计算形状值或其他跟踪时间常量。请参阅下面的代码块,快速了解示例,并详细了解其他问题,请参阅“开启全面暂存可能导致哪些问题?”部分。
现在改为:
@jit
def f(x):
input_size = jnp.prod(x.shape)
if input_size > 100:
…
请执行以下操作:
import numpy as np
@jit
def f(x):
input_size = np.prod(x.shape)
if input_size > 100:
…
现在不再将 jax.numpy 视为 numpy 的可替代品,现在最好仅在需要在加速器(如 GPU)上执行计算时才考虑使用 jax.numpy 操作。
“全面暂存”是什么以及其有何用处?
全面暂存是 JAX 核心升级的名称,旨在从逐操作的 Python 到 XLA 分阶段进行计算,并避免在 jit、pmap 和控制流原语中进行“跟踪时间常量折叠”。因此,全面暂存通过减少跟踪过程中的碎片化和生成更少的 XLA 编译时常量(有时会显著降低)来改善 JAX 的内存性能。它还可以通过在跟踪时间消除逐操作执行来改善跟踪性能。此外,全面暂存简化了 JAX 核心内部结构,修复了许多未解决的 bug,并为重要的即将推出的功能铺平了道路。
名称“全面暂存”意味着尽可能分阶段输出所有内容。
玩具示例
像jit和pmap这样的 JAX 变换将计算分阶段到 XLA。也就是说,我们将它们应用于由多个原始操作组成的函数,使得这些操作不再从 Python 中逐个执行,而是作为一个端到端优化的 XLA 计算的一部分。
但确切地说哪些操作被分阶段了?在全阶段之前,JAX 仅基于数据依赖性分阶段计算。这里有一个示例函数,后面是它在全阶段更改之前分阶段的 XLA HLO 程序:
from jax import jit
import jax.numpy as jnp
@jit
def f(x):
y = jnp.add(1, 1)
return x * y
f(3)
ENTRY jit_f.6 {
constant.2 = pred[] constant(false)
parameter.1 = s32[] parameter(0)
constant.3 = s32[] constant(2)
multiply.4 = s32[] multiply(parameter.1, constant.3)
ROOT tuple.5 = (s32[]) tuple(multiply.4)
}
注意,add操作没有被分阶段。相反,我们只看到一个乘法。
这是从这个函数生成的 HLO,在全阶段更改之后:
ENTRY jit_f.8 {
constant.2 = pred[] constant(false)
parameter.1 = s32[] parameter(0)
constant.3 = s32[] constant(1)
constant.4 = s32[] constant(1)
add.5 = s32[] add(constant.3, constant.4)
multiply.6 = s32[] multiply(parameter.1, add.5)
ROOT tuple.7 = (s32[]) tuple(multiply.6)
}
稍微不那么玩具的示例
这里是在实践中可能出现的一个不那么玩具的示例,当我们想要创建布尔掩码时:
import jax.numpy as jnp
from jax import lax
@jit
def select_tril(x):
mask = jnp.arange(x.shape[0])[:, None] > jnp.arange(x.shape[1])
return lax.select(mask, x, jnp.zeros_like(x)) # lax.select is like jnp.where
x = np.arange(12).reshape((3, 4))
select_tril(x)
在全阶段之前:
ENTRY jit_select_tril.8 {
constant.3 = pred[] constant(false)
constant.1 = pred[3,4]{1,0} constant({…})
parameter.2 = s32[3,4]{1,0} parameter(0)
constant.4 = s32[] constant(0)
broadcast.5 = s32[3,4]{1,0} broadcast(constant.4), dimensions={}
select.6 = s32[3,4]{1,0} select(constant.1, parameter.2, broadcast.5)
ROOT tuple.7 = (s32[3,4]{1,0}) tuple(select.6)
}
select操作被分阶段了,但用于构建常量mask的操作却没有。而不是被分阶段,构建mask的操作在 Python 追踪时逐个操作地执行,并且 XLA 只看到一个编译时常量constant.1,表示mask的值。这是不幸的,因为如果我们已经分阶段了构建mask的操作,XLA 可以将它们融合到select中,并避免完全实现结果。因此,我们最终会浪费内存,因为一个可能很大的常量,浪费时间分派多个未融合的逐个操作的 XLA 计算,甚至可能会导致内存碎片化。
(与为jnp.zeros_like(x)构建零数组的广播相对应的操作被分阶段,因为 JAX 对来自google/jax#1668的非常简单表达式很懒惰。在全阶段之后,我们可以去掉那个懒惰的子语言,并简化 JAX 内部。)
创建mask的原因不被分阶段的原因是,在全阶段之前,jit基于数据依赖性运行。也就是说,jit仅分阶段一个函数中对参数有数据依赖性的操作。控制流基元和pmap的行为类似。在select_tril的情况下,用于构建常量mask的操作与参数 x 没有数据依赖关系,因此它们不会被分阶段;只有lax.select调用具有数据依赖性。
使用全阶段后,jit转换函数的动态上下文中的所有jax.numpy调用都被分阶段到 XLA。也就是说,在全阶段后,select_tril的计算 XLA 看到的是
ENTRY jit_select_tril.16 {
constant.4 = pred[] constant(false)
iota.1 = s32[3]{0} iota(), iota_dimension=0
broadcast.5 = s32[3,1]{1,0} broadcast(iota.1), dimensions={0}
reshape.7 = s32[3]{0} reshape(broadcast.5)
broadcast.8 = s32[3,4]{1,0} broadcast(reshape.7), dimensions={0}
iota.2 = s32[4]{0} iota(), iota_dimension=0
broadcast.6 = s32[1,4]{1,0} broadcast(iota.2), dimensions={1}
reshape.9 = s32[4]{0} reshape(broadcast.6)
broadcast.10 = s32[3,4]{1,0} broadcast(reshape.9), dimensions={1}
compare.11 = pred[3,4]{1,0} compare(broadcast.8, broadcast.10), direction=GT
parameter.3 = s32[3,4]{1,0} parameter(0)
constant.12 = s32[] constant(0)
broadcast.13 = s32[3,4]{1,0} broadcast(constant.12), dimensions={}
select.14 = s32[3,4]{1,0} select(compare.11, parameter.3, broadcast.13)
ROOT tuple.15 = (s32[3,4]{1,0}) tuple(select.14)
}
当全阶段打开时可能会出现哪些问题?
当在jit或pmap的动态上下文中,从 Python 到 XLA 分阶段所有jax.numpy操作的结果,一些之前正常工作的代码可能会开始引发大声的错误。正如下文所解释的那样,这些行为在全阶段之前已经存在 bug,但全阶段将它们变成了严格的错误。
使用jax.numpy进行形状计算
示例
from jax import jit
import jax.numpy as jnp
@jit
def ex1(x):
size = jnp.prod(jnp.array(x.shape))
return x.reshape((size,))
ex1(jnp.ones((3, 4)))
错误消息
[… full traceback …]
File \”/home/mattjj/packages/jax/jax/core.py\”, line 862, in raise_concretization_error
raise ConcretizationTypeError(msg)
jax.core.ConcretizationTypeError: Abstract tracer value encountered where concrete value is expected.
The error arose in jax.numpy.reshape.
While tracing the function ex1 at ex1.py:4, this value became a tracer due to JAX operations on these lines:
operation c:int32[] = reduce_prod[ axes=(0,) ] b:int32[2]
from line ex1.py:6 (ex1)
You can use transformation parameters such as `static_argnums` for `jit` to avoid tracing particular arguments of transformed functions.
See https://jax.readthedocs.io/en/latest/faq.html#abstract-tracer-value-encountered-where-concrete-value-is-expected-error for more information.
Encountered tracer value: Traced<ShapedArray(int32[])>with<DynamicJaxprTrace(level=0/1)>
解释
在全面化下,我们不能像上面使用jnp.prod一样在 jit 函数的动态上下文中使用jax.numpy进行形状计算,因为这些操作将被分阶段为在执行时计算的值,但我们需要它们是编译时常量(因此是跟踪时常量)。
在全面化之前,这段代码不会引发错误,但这是一个常见的性能 bug:jnp.prod计算将在跟踪时间在设备上执行,意味着额外的编译、传输、同步、分配和潜在的内存碎片化。
解决方案
解决方法很简单,就是像这样的形状计算使用原始的numpy。这不仅避免了错误,还将计算保持在主机上(并且开销更低)。
在代码中,这个问题很常见,我们努力使错误消息尤其好。除了堆栈跟踪显示抽象跟踪器值导致问题的位置(完整堆栈跟踪中的jnp.reshape行,在 omni.py:10),我们还解释了这个值首先变成跟踪器的原因,指向导致它成为抽象跟踪器的上游原始操作(来自jnp.prod中的reduce_prod,在 omni.py:9),以及跟踪器属于哪个带jit装饰的函数(在 omni.py:6 中的ex1)。
副作用
示例
from jax import jit
from jax import random
key = random.PRNGKey(0)
def init():
global key
key, subkey = random.split(key)
return random.normal(subkey, ())
print(init()) # -1.2515389
print(init()) # -0.58665067
init = jit(init)
print(init()) # 0.48648298
print(init()) # 0.48648298 !!
最后一个调用具有重复的随机性,但没有硬错误,因为我们没有重新执行 Python。但是如果我们查看key,我们会看到一个逃逸的跟踪器开启全面化时:
print(key) # Traced<ShapedArray(uint32[2])>with<DynamicJaxprTrace(level=0/1)>
在全面化之前,random.split调用不会被分阶段处理,因此我们不会得到逃逸的跟踪器。由于重复使用相同的 PRNG 密钥,代码仍然存在 bug,即编译函数无法复制原始函数的语义(因为有副作用)。
在开启全面化时,如果再次触及key,将会得到一个逃逸的跟踪器错误:
random.normal(key, ())
错误消息
[… full stack trace …]
File \”/home/mattjj/packages/jax/jax/interpreters/partial_eval.py\”, line 836, in _assert_live
raise core.escaped_tracer_error(msg)
jax.core.UnexpectedTracerError: Encountered an unexpected tracer. Perhaps this tracer escaped through global state from a previously traced function.
The functions being transformed should not save traced values to global state. Detail: tracer created on line example.py:8 (init).
解释
我们发现的次大类全面化问题与副作用代码有关。这些代码通过转换有副作用的函数已经使 JAX 的保证失效,但由于预全面化的“跟踪时间常数折叠”行为,一些有副作用的函数仍然可能表现正确。全面化能更多地捕捉这些错误。
解决方案
解决方法是识别依赖副作用的 JAX 转换函数,并重新编写它们以避免有副作用。
基于 XLA 优化的小数值差异
因为在全面化下,更多的计算被分阶段到 XLA,而不是在跟踪时间执行,这可能导致浮点运算的重新排序。结果是,我们看到数值行为以一种导致测试在开启全面化时失败的方式改变,因为它们对于过紧容差的测试失败。
依赖于 JAX 内部 API 的变化
Omnistaging 涉及对 JAX 核心代码进行了一些重大修改,包括删除或更改内部函数。任何依赖这些内部 JAX API 的代码,在 omnistaging 打开时都可能会出现问题,可能是构建错误(来自 pytype)或运行时错误。
触发 XLA 编译时错误
由于 omnistaging 涉及将更多代码分阶段传递给 XLA,我们发现它可能会在某些后端触发现有的 XLA 编译时错误。对于这些问题,最好的做法是报告它们,以便我们与 XLA 团队合作进行修复。
JEP 9263:类型化密钥和可插拔的 RNG
原文:jax.readthedocs.io/en/latest/jep/9263-typed-keys.html
Jake VanderPlas, Roy Frostig
August 2023
概述
未来,在 JAX 中,RNG 密钥将更加类型安全和可定制。 不再通过长度为 2 的uint32数组表示单个 PRNG 密钥,而是通过一个标量数组表示,该数组具有满足jnp.issubdtype(key.dtype, jax.dtypes.prng_key)的特殊 RNG dtype。
目前,可以使用jax.random.PRNGKey()仍然创建旧样式的 RNG 密钥:
>>> key = jax.random.PRNGKey(0)
>>> key
Array([0, 0], dtype=uint32)
>>> key.shape
(2,)
>>> key.dtype
dtype(\’uint32\’)
从现在开始,可以使用jax.random.key()创建新样式的 RNG 密钥:
>>> key = jax.random.key(0)
>>> key
Array((), dtype=key<fry>) overlaying:
[0 0]
>>> key.shape
()
>>> key.dtype
key<fry>
这个(标量形状的)数组的行为与任何其他 JAX 数组相同,只是其元素类型是一个密钥(及其关联的元数据)。 我们也可以制作非标量密钥数组,例如通过将jax.vmap()应用于jax.random.key():
>>> key_arr = jax.vmap(jax.random.key)(jnp.arange(4))
>>> key_arr
Array((4,), dtype=key<fry>) overlaying:
[[0 0]
[0 1]
[0 2]
[0 3]]
>>> key_arr.shape
(4,)
除了切换到新的构造函数外,大多数与 PRNG 相关的代码应该继续按预期工作。 您可以像以前一样继续使用jax.random API 中的密钥;例如:
# split
new_key, subkey = jax.random.split(key)
# random number generation
data = jax.random.uniform(key, shape=(5,))
然而,并非所有数值操作都适用于密钥数组。 它们现在故意引发错误:
>>> key = key + 1
Traceback (most recent call last):
TypeError: add does not accept dtypes key<fry>, int32.
如果出于某种原因您需要恢复底层缓冲区(旧样式密钥),您可以使用jax.random.key_data()来实现:
>>> jax.random.key_data(key)
Array([0, 0], dtype=uint32)
对于旧样式密钥,key_data()是一个身份操作。
对用户来说,这意味着什么?
对于 JAX 用户,这种变化现在不需要任何代码更改,但我们希望您会发现升级是值得的,并切换到使用类型化密钥。 要尝试这个功能,请将使用jax.random.PRNGKey()替换为jax.random.key()。 这可能会在您的代码中引入一些破坏性变化,属于以下几类之一:
如果您的代码对密钥执行不安全/不支持的操作(如索引、算术运算、转置等;请参阅下面的类型安全部分),这种变化将捕捉到它。 您可以更新您的代码以避免此类不支持的操作,或者使用jax.random.key_data()和jax.random.wrap_key_data()以不安全的方式操作原始密钥缓冲区。
如果您的代码包含关于key.shape的显式逻辑,您可能需要更新此逻辑以考虑尾部密钥缓冲区维度不再是形状的显式部分。
如果您的代码包含关于key.dtype的显式逻辑,您需要将其升级为使用新的公共 API 来推理 RNG dtypes,例如dtypes.issubdtype(dtype, dtypes.prng_key)。
如果您调用一个尚未处理类型化 PRNG 密钥的基于 JAX 的库,您现在可以使用raw_key = jax.random.key_data(key)来恢复原始缓冲区,但请务必保留一个 TODO 来在下游库支持类型化 RNG 密钥后移除此操作。
在未来的某个时候,我们计划废弃jax.random.PRNGKey()并要求使用jax.random.key()。
检测新样式的类型化密钥
要检查对象是否为新样式的类型化 PRNG 密钥,可以使用jax.dtypes.issubdtype或jax.numpy.issubdtype:
>>> typed_key = jax.random.key(0)
>>> jax.dtypes.issubdtype(typed_key.dtype, jax.dtypes.prng_key)
True
>>> raw_key = jax.random.PRNGKey(0)
>>> jax.dtypes.issubdtype(raw_key.dtype, jax.dtypes.prng_key)
False
PRNG 密钥的类型注释
旧式和新式 PRNG 密钥的推荐类型注释是 jax.Array。PRNG 密钥根据其dtype与其他数组区分开来,目前无法在类型注释中指定 JAX 数组的 dtype。以前可以使用jax.random.KeyArray或jax.random.PRNGKeyArray作为类型注释,但在类型检查下始终被别名为Any,因此jax.Array具有更高的特异性。
注:在 JAX 版本 0.4.16 中,jax.random.KeyArray 和 jax.random.PRNGKeyArray 已弃用,并在 JAX 版本 0.4.24 中移除。
JAX 库作者注意事项
如果您维护基于 JAX 的库,您的用户也是 JAX 用户。请知道 JAX 将继续支持“原始”旧式密钥在jax.random中,因此调用者可能期望它们在所有地方都被接受。如果您希望在您的库中要求新式类型化密钥,则可能希望使用以下方式进行检查以强制执行它们:
from jax import dtypes
def ensure_typed_key_array(key: Array) -> Array:
if dtypes.issubdtype(key.dtype, dtypes.prng_key):
return key
else:
raise TypeError(\”New-style typed JAX PRNG keys required\”)
动机
此更改的两个主要动机因素是可定制性和安全性。
自定义 PRNG 实现
JAX 目前使用单一的全局配置 PRNG 算法。PRNG 密钥是无符号 32 位整数的向量,jax.random API 使用它们生成伪随机流。任何更高秩的 uint32 数组都被解释为具有这些密钥缓冲区的数组,其中尾部维度表示密钥。
这种设计的缺点在我们引入替代的伪随机数生成器(PRNG)实现时变得更加明显,这些实现必须通过设置全局或本地配置标志来选择。不同的 PRNG 实现具有不同大小的密钥缓冲区和生成随机比特的不同算法。通过全局标志确定此行为容易出错,特别是在整个进程中使用多个密钥实现时。
我们的新方法是将实现作为 PRNG 密钥类型的一部分,即密钥数组的元素类型。使用新的密钥 API,下面是在默认的 threefry2x32 实现(纯 Python 实现,并与 JAX 编译)和非默认的 rbg 实现(对应单个 XLA 随机比特生成操作)下生成伪随机值的示例:
>>> key = jax.random.key(0, impl=\’threefry2x32\’) # this is the default impl
>>> key
Array((), dtype=key<fry>) overlaying:
[0 0]
>>> jax.random.uniform(key, shape=(3,))
Array([0.9653214 , 0.31468165, 0.63302994], dtype=float32)
>>> key = jax.random.key(0, impl=\’rbg\’)
>>> key
Array((), dtype=key<rbg>) overlaying:
[0 0 0 0]
>>> jax.random.uniform(key, shape=(3,))
Array([0.39904642, 0.8805201 , 0.73571277], dtype=float32)
安全的 PRNG 密钥使用
原则上,PRNG 密钥确实只支持少数几种操作,即密钥衍生(例如拆分)和随机数生成。只要正确拆分密钥并且每个密钥只使用一次,PRNG 就设计为生成独立的伪随机数。
在其他方式中操作或消耗密钥数据的代码通常表明是意外的错误,将密钥数组表示为原始 uint32 缓冲区已经允许沿着这些方向容易发生误用。以下是我们在实际使用中遇到的几个示例错误用法:
密钥缓冲区索引
访问底层整数缓冲区使得可以轻松尝试以非标准方式导出密钥,有时会带来意想不到的不良后果:
# Incorrect
key = random.PRNGKey(999)
new_key = random.PRNGKey(key[1]) # identical to the original key!
# Correct
key = random.PRNGKey(999)
key, new_key = random.split(key)
如果此关键是使用random.key(999)创建的新型类型化关键,则索引到关键缓冲区将会出错。
关键算术
关键算术是从其他关键派生关键的一种类似险恶的方式。通过直接操作关键数据而避免jax.random.split()或jax.random.fold_in()来派生关键,会产生一批关键,这些关键——根据 PRNG 实现——可能会在批次内生成相关的随机数:
# Incorrect
key = random.PRNGKey(0)
batched_keys = key + jnp.arange(10, dtype=key.dtype)[:, None]
# Correct
key = random.PRNGKey(0)
batched_keys = random.split(key, 10)
使用random.key(0)创建的新型类型化关键通过禁止对关键进行算术操作来解决这个问题。
意外转置关键缓冲区
使用“原始”旧式关键数组时,很容易意外交换批次(前导)维度和关键缓冲区(尾随)维度。再次可能导致产生相关伪随机性的关键。多年来我们见过的一个模式归结如下:
# Incorrect
keys = random.split(random.PRNGKey(0))
data = jax.vmap(random.uniform, in_axes=1)(keys)
# Correct
keys = random.split(random.PRNGKey(0))
data = jax.vmap(random.uniform, in_axes=0)(keys)
这里的 bug 很微妙。通过在 in_axes=1 上映射,此代码通过将批次中每个关键缓冲区的单个元素组合成新关键来生成新关键。生成的关键彼此不同,但实质上以非标准方式“派生”。再次强调,PRNG 并未设计或测试以从这样的关键批次生成独立的随机流。
使用random.key(0)创建的新型类型化关键通过隐藏个体关键的缓冲区表示,而将关键视为关键数组的不透明元素来解决这个问题。关键数组没有尾随的“缓冲区”维度可以索引、转置或映射。
关键重用
不像像numpy.random这样的基于状态的 PRNG API,JAX 的函数式 PRNG 在使用后不会隐式更新关键。
# Incorrect
key = random.PRNGKey(0)
x = random.uniform(key, (100,))
y = random.uniform(key, (100,)) # Identical values!
# Correct
key = random.PRNGKey(0)
key1, key2 = random.split(random.key(0))
x = random.uniform(key1, (100,))
y = random.uniform(key2, (100,))
我们正在积极开发工具来检测和防止意外的关键重用。这仍然是一个正在进行中的工作,但它依赖于类型化关键数组。现在升级到类型化关键使我们能够在构建这些安全功能时引入它们。
类型化 PRNG 关键的设计
类型化 PRNG 关键在 JAX 中实现为扩展 dtypes 的实例,其中新的 PRNG dtypes 是子 dtype。
扩展 dtypes
从用户角度来看,扩展 dtype dt 具有以下用户可见属性:
jax.dtypes.issubdtype(dt, jax.dtypes.extended) 返回 True:这是应该用于检测 dtype 是否为扩展 dtype 的公共 API。
它具有类级属性dt.type,返回在numpy.generic层次结构中的类型类。这类似于np.dtype(\’int32\’).type返回numpy.int32,这不是 dtype 而是标量类型,并且是numpy.generic的子类。
与 numpy 标量类型不同,我们不允许实例化dt.type标量对象:这符合 JAX 将标量值表示为零维数组的决定。
从非公开实现的角度来看,扩展 dtype 具有以下属性:
它的类型是私有基类jax._src.dtypes.ExtendedDtype的子类,这是用于扩展数据类型的非公开基类。ExtendedDtype的实例类似于np.dtype的实例,例如np.dtype(\’int32\’)。
它具有私有的_rules属性,允许数据类型定义在特定操作下的行为方式。例如,当dtype是扩展数据类型时,jax.lax.full(shape, fill_value, dtype)将委托给dtype._rules.full(shape, fill_value, dtype)。
为什么要在一般情况下引入扩展数据类型,超出了伪随机数生成器的范围?我们在内部的其他地方重复使用同样的扩展数据类型机制。例如,jax._src.core.bint对象是另一种扩展数据类型,用于动态形状的实验工作。在最近的 JAX 版本中,它满足上述属性(见jax/_src/core.py#L1789-L1802)。
PRNG 数据类型
PRNG 数据类型被定义为扩展数据类型的特例。具体来说,此更改引入了一个新的公共标量类型类jax.dtypes.prng_key,其具有以下属性:
>>> jax.dtypes.issubdtype(jax.dtypes.prng_key, jax.dtypes.extended)
True
PRNG 密钥数组然后具有以下属性的数据类型:
>>> key = jax.random.key(0)
>>> jax.dtypes.issubdtype(key.dtype, jax.dtypes.extended)
True
>>> jax.dtypes.issubdtype(key.dtype, jax.dtypes.prng_key)
True
除了一般情况下扩展数据类型的key.dtype._rules,PRNG 数据类型定义了key.dtype._impl,其中包含定义 PRNG 实现的元数据。当前,PRNGImpl并不打算成为公共 API,但我们可能很快会重新审视这一点,以允许完全自定义的 PRNG 实现。
进展
以下是实施上述设计的关键拉取请求的非全面列表。主要的跟踪问题是#9263。
通过PRNGImpl实现可插拔 PRNG:#6899
实现PRNGKeyArray,不包括数据类型:#11952
向PRNGKeyArray添加一个“自定义元素”数据类型属性,具有_rules属性:#12167
将“自定义元素类型”重命名为“不透明数据类型”:#12170
重构bint以使用不透明数据类型基础设施:#12707
添加jax.random.key以直接创建带类型的密钥:#16086
为key和PRNGKey添加impl参数:#16589
将“不透明数据类型”重命名为“扩展数据类型”,并定义jax.dtypes.extended:#16824
引入jax.dtypes.prng_key并统一 PRNG 数据类型和扩展数据类型:#16781
添加一个jax_legacy_prng_key标志,以支持在使用传统(原始)PRNG 密钥时发出警告或错误:#17225
JAX 类型提升的设计
原文:jax.readthedocs.io/en/latest/jep/9407-type-promotion.html
Jake VanderPlas, December 2021
任何数值计算库设计中面临的挑战之一是如何处理不同类型值之间的操作选择。本文概述了 JAX 使用的提升语义背后的思维过程,总结在JAX 类型提升语义中。
JAX 类型提升的目标
JAX 的数值计算 API 是模仿 NumPy 的,但增加了一些功能,包括能够针对 GPU 和 TPU 等加速器进行优化。这使得采用 NumPy 的类型提升系统对 JAX 用户不利:NumPy 的类型提升规则严重偏向于 64 位输出,这对于加速器上的计算是有问题的。像 GPU 和 TPU 这样的设备通常需要付出显著的性能代价来使用 64 位浮点类型,并且在某些情况下根本不支持本地 64 位浮点类型。
这种问题类型提升语义的简单例子可以在 32 位整数和浮点数之间的二进制操作中看到:
import numpy as np
np.dtype(np.int32(1) + np.float32(1))
dtype(\’float64\’)
NumPy 倾向于生成 64 位值是使用 NumPy API 进行加速计算的一个长期问题,目前还没有一个很好的解决方案。因此,JAX 已经开始重新思考以加速器为目标的 NumPy 风格类型提升。
回顾:表格和格子
在我们深入细节之前,让我们花点时间退后一步,思考如何思考类型提升问题。考虑 Python 内置数值类型(即int、float和complex)之间的算术操作,我们可以用几行代码生成 Python 用于这些类型值加法的类型提升表:
import pandas as pd
types = [int, float, complex]
name = lambda t: t.__name__
pd.DataFrame([[name(type(t1(1) + t2(1))) for t1 in types] for t2 in types],
index=[name(t) for t in types], columns=[name(t) for t in types])
intfloatcomplexintintfloatcomplexfloatfloatfloatcomplexcomplexcomplexcomplexcomplex
这张表详细列出了 Python 的数值类型提升行为,但事实证明有一种更为简洁的补充表示:格表示法,其中任意两个节点之间的上确界是它们提升到的类型。Python 提升表的格表示法要简单得多:
显示代码单元格源代码 隐藏代码单元格源代码
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {\’int\’: [\’float\’], \’float\’: [\’complex\’]}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {\’int\’: [0, 0], \’float\’: [1, 0], \’complex\’: [2, 0]}
fig, ax = plt.subplots(figsize=(8, 2))
nx.draw(graph, with_labels=True, node_size=4000, node_color=\’lightgray\’, pos=pos, ax=ax, arrowsize=20)
“`</details> 
这个格是促进表中信息的紧凑编码。您可以通过跟踪到两个节点的第一个共同子节点(包括节点本身)找到两个输入的类型提升的结果;在数学上,这个共同子节点被称为对格上的*上确界*,或*最小上界*,或*结合*的操作;这里我们将这个操作称为**结合**。
概念上,箭头表示允许在源和目标之间进行*隐式类型提升*:例如,允许从整数到浮点数的隐式提升,但不允许从浮点数到整数的隐式提升。
请记住,通常并非每个有向无环图(DAG)都满足格的性质。格要求每对节点之间存在唯一的最小上界;例如,以下两个 DAG 不是格:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源码 隐藏代码单元格源码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 2, figsize=(10, 2))
lattice = {\’A\’: [\’B\’, \’C\’]}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {\’A\’: [0, 0], \’B\’: [1, 0.5], \’C\’: [1, -0.5]}
nx.draw(graph, with_labels=True, node_size=2000, node_color=\’lightgray\’, pos=pos, ax=ax[0], arrowsize=20)
ax[0].set(xlim=[-0.5, 1.5], ylim=[-1, 1])
lattice = {\’A\’: [\’C\’, \’D\’], \’B\’: [\’C\’, \’D\’]}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {\’A\’: [0, 0.5], \’B\’: [0, -0.5], \’C\’: [1, 0.5], \’D\’: [1, -0.5]}
nx.draw(graph, with_labels=True, node_size=2000, node_color=\’lightgray\’, pos=pos, ax=ax[1], arrowsize=20)
ax[1].set(xlim=[-0.5, 1.5], ylim=[-1, 1]);
“`</details> 
左边的 DAG 不是格,因为节点`B`和`C`没有上界;右边的 DAG 有两个问题:首先,节点`C`和`D`没有上界,其次,节点`A`和`B`的最小上界无法*唯一*确定:`C`和`D`都是候选项,但它们是不可排序的。
### 类型提升格的属性
在格中指定类型提升确保了许多有用的属性。用\\(\\vee\\)运算符表示格中的结合,我们有:
**存在性:** 格的定义要求每对元素都存在唯一的格结合:\\(\\forall (a, b): \\exists !(a \\vee b)\\)
**交换律:** 格的结合运算是交换的:\\(\\forall (a, b): a\\vee b = b \\vee a\\).
**结合律:** 格的结合运算是结合的:\\(\\forall (a, b, c): a \\vee (b \\vee c) = (a \\vee b) \\vee c\\).
另一方面,这些属性意味着它们对能够表示的类型提升系统有所限制;特别是**并非每个类型提升表都可以用格表示**。NumPy 的完整类型提升表就是一个快速反例:这里有三种标量类型,它们在 NumPy 中的提升行为是非结合的。
“`py
import numpy as np
a, b, c = np.int8(1), np.uint8(1), np.float16(1)
print(np.dtype((a + b) + c))
print(np.dtype(a + (b + c)))
float32
float16
这样的结果可能会让用户感到惊讶:我们通常期望数学表达式映射到数学概念,所以,例如,a + b + c应等同于c + b + a;x * (y + z)应等同于x * y + x * z。如果类型提升不是结合的或不是交换的,这些属性将不再适用。
此外,基于格子的类型提升系统与基于表的系统相比,在概念上更简单和更易理解。例如,JAX 识别 18 种不同的类型:一个包含 18 个节点和之间稀疏、有充分动机的连接的提升格子,比 324 个条目的表在脑中更容易维持。
因此,我们选择为 JAX 使用基于格子的类型提升系统。
类别内的类型提升
数值计算库通常提供不仅仅是int、float和complex,在每个类别中,都有各种可能的精度,由数值表示中使用的位数表示。我们在这里考虑的类别是:
无符号整数,包括uint8、uint16、uint32和uint64(我们简称为u8、u16、u32、u64)
有符号整数,包括int8、int16、int32和int64(我们简称为i8、i16、i32、i64)
浮点数,包括float16、float32和float64(我们简称为f16、f32、f64)
复数浮点数,包括complex64和complex128(我们简称为c64、c128)
Numpy 在每个这四个类别内的类型提升语义相对来说是相对简单的:类型的有序层次结构直接转换为四个分离的格子,表示类内类型提升规则:
显示代码单元源代码 隐藏代码单元源代码
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’u8\’: [\’u16\’], \’u16\’: [\’u32\’], \’u32\’: [\’u64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’u8\’: [0, 0], \’u16\’: [1, 0], \’u32\’: [2, 0], \’u64\’: [3, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [1, 2], \’f32\’: [2, 2], \’f64\’: [3, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 4))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 
关于 JAX 避免的值提升为 64 位,这些同类别的提升语义在每种类型类别内部是没有问题的:产生 64 位输出的唯一方式是有一个 64 位输入。
## 输入 Python 标量
现在让我们考虑 Python 标量如何融入其中。
在 NumPy 中,提升行为取决于输入是数组还是标量。例如,在操作两个标量时,适用正常的提升规则:
“`py
x = np.int8(0) # int8 scalar
y = 1 # Python int = int64 scalar
(x + y).dtype
dtype(\’int64\’)
在这里,Python 值1被视为int64,并且简单的类内规则导致int64结果。
然而,在 Python 标量和 NumPy 数组之间的操作中,标量会延续到数组的 dtype。例如:
x = np.zeros(1, dtype=\’int8\’) # int8 array
y = 1 # Python int = int64 scalar
(x + y).dtype
dtype(\’int8\’)
忽略int64标量的位宽度,而是延续数组的位宽度。
这里还有一个细节:当 NumPy 类型提升涉及标量时,输出的 dtype 取决于值:如果 Python 标量过大,超出了给定 dtype 的范围,则被提升为兼容的类型:
x = np.zeros(1, dtype=\’int8\’) # int8 array
y = 1000 # int64 scalar
(x + y).dtype
dtype(\’int16\’)
出于 JAX 的目的,依赖值的提升是不可行的,因为 JIT 编译和其他转换的性质使其作用于数据的抽象表示,而不参考其值。
忽略依赖值的影响,NumPy 类型提升的有符号整数分支可以在以下格点中表示,我们将使用 * 标记标量数据类型:
显示代码单元格来源 隐藏代码单元格来源
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i8*\’: [\’i16*\’], \’i16*\’: [\’i32*\’], \’i32*\’: [\’i64*\’], \’i64*\’: [\’i8\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i8*\’: [0, 1], \’i16*\’: [2, 1], \’i32*\’: [4, 1], \’i64*\’: [6, 1],
\’i8\’: [9, 1], \’i16\’: [11, 1], \’i32\’: [13, 1], \’i64\’: [15, 1],
}
fig, ax = plt.subplots(figsize=(12, 4))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
ax.text(3, 1.6, \”Scalar Types\”, ha=\’center\’, fontsize=14)
ax.text(12, 1.6, \”Array Types\”, ha=\’center\’, fontsize=14)
ax.set_ylim(-1, 3);
“`</details> 
在 `uint`、`float` 和 `complex` 格点内,类似的模式也成立。
为了简单起见,让我们将每个标量类型的类别折叠为单个节点,分别表示为 `u*`、`i*`、`f*` 和 `c*`。我们的类别内格点集现在可以这样表示:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格来源 隐藏代码单元格来源</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’u*\’: [\’u8\’], \’u8\’: [\’u16\’], \’u16\’: [\’u32\’], \’u32\’: [\’u64\’],
\’i*\’: [\’i8\’], \’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’],
\’f*\’: [\’f16\’], \’f16\’: [\’f32\’], \’f32\’: [\’f64\’],
\’c*\’: [\’c64\’], \’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’u*\’: [0, 0], \’u8\’: [3, 0], \’u16\’: [5, 0], \’u32\’: [7, 0], \’u64\’: [9, 0],
\’i*\’: [0, 1], \’i8\’: [3, 1], \’i16\’: [5, 1], \’i32\’: [7, 1], \’i64\’: [9, 1],
\’f*\’: [0, 2], \’f16\’: [5, 2], \’f32\’: [7, 2], \’f64\’: [9, 2],
\’c*\’: [0, 3], \’c64\’: [7, 3], \’c128\’: [9, 3],
}
fig, ax = plt.subplots(figsize=(6, 4))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 
从某种意义上说,将标量放在左边是一个奇怪的选择:标量类型可能包含任何宽度的值,但与给定类型的数组交互时,提升的结果将延续到数组类型。这样做的好处在于,当您对数组 `x` 执行像 `x + 2` 这样的操作时,`x` 的类型将传递到结果中,无论其宽度如何:
“`py
for dtype in [np.int8, np.int16, np.int32, np.int64]:
x = np.arange(10, dtype=dtype)
assert (x + 2).dtype == dtype
这种行为为标量值的 * 符号赋予了动机:* 符号类似于一个通配符,可以取任意所需的值。
这种语义的好处在于,您可以用清晰的 Python 代码轻松表达操作序列,而无需显式地将标量强制转换为适当的类型。想象一下,如果不是写成这样:
3 * (x + 1) ** 2
您不得不写成这样:
np.int32(3) * (x + np.int32(1)) ** np.int32(2)
尽管它很明确,数值代码会变得阅读或编写起来非常繁琐。使用上述标量提升语义,给定类型为 int32 的数组 x,第二个语句中的类型在第一个语句中是隐含的。
合并格点
请回想,我们开始讨论 Python 内部类型提升的格点图:int -> float -> complex。让我们将其重写为 i* -> f* -> c*,并允许 i* 吸收 u*(毕竟,在 Python 中没有无符号整数标量类型)。
将所有内容整合在一起,我们得到以下部分格点图,表示 Python 标量和 numpy 数组之间的类型提升:
显示代码单元格来源 隐藏代码单元格来源
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’], \’u16\’: [\’u32\’], \’u32\’: [\’u64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [0.5, 2], \’f32\’: [1.5, 2], \’f64\’: [2.5, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 
注意,这还不是一个真正的格:存在许多节点对,它们之间没有联接。然而,我们可以将其视为一个*部分*格,在这种格中,某些节点对没有定义的推广行为,而此部分格的定义部分确实正确描述了 NumPy 的数组推广行为(不考虑上述值依赖语义)。
这为我们提供了一个很好的框架,可以用来思考如何填补这些未定义的推广规则,方法是在这个图上添加连接。但是应该添加哪些连接呢?总体来说,我们希望任何额外的连接都满足几个属性:
1. 推广应满足交换和结合性质:换句话说,图应保持(部分)格的形式。
1. 推广不应允许丢弃数据的整个组成部分:例如,我们不应将`complex`推广为`float`,因为这会丢弃任何虚部。
1. 推广不应导致未处理的溢出。例如,最大可能的`uint32`是最大可能的`int32`的两倍,因此我们不应隐式地将`uint32`提升为`int32`。
1. 在可能的情况下,推广应避免精度损失。例如,一个`int64`值可能有 64 位的尾数,因此将`int64`提升为`float64`可能会导致精度损失。然而,最大可表示的 float64 大于最大可表示的 int64,因此在这种情况下仍满足标准 #3。
1. 在可能的情况下,二进制推广应避免导致比输入更宽的类型。这是为了确保 JAX 的隐式推广对加速器工作流友好,其中用户通常希望将类型限制为 32 位(或在某些情况下是 16 位)值。
格上的每一个新连接都为用户引入了一定程度的便利性(一组新的可以在没有显式转换的情况下相互作用的类型),但是如果以上任何标准被违反,这种便利性可能会变得代价高昂。发展一个完整的推广格涉及在便利性和成本之间达到平衡。
## 混合推广:浮点数和复数
让我们从可能是最简单的情况开始,即在浮点数和复数值之间的推广。
复数由一对浮点数组成,因此在它们之间存在一种自然的推广路径:将浮点数转换为复数,同时保持实部的宽度。在我们的部分格表示中,它看起来像这样:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源码 隐藏代码单元格源码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’], \’u16\’: [\’u32\’], \’u32\’: [\’u64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [0.5, 2], \’f32\’: [1.5, 2], \’f64\’: [2.5, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 
这恰好代表了 Numpy 在混合浮点/复数类型推广中使用的语义。
## 混合推广:有符号和无符号整数
接下来的情况,让我们考虑一些更困难的情况:有符号和无符号整数之间的提升。例如,当将`uint8`提升为有符号整数时,我们需要多少位?
乍一看,您可能会认为将`uint8`提升为`int8`是很自然的;但最大的`uint8`数字在`int8`中是不能表示的。因此,将无符号整数提升为比特数加倍的整数更有意义;这种提升行为可以通过将以下连接添加到提升格中来表示:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源代码 隐藏代码单元格源代码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [0.5, 2], \’f32\’: [1.5, 2], \’f64\’: [2.5, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 
同样,这里添加的连接正是 NumPy 用于混合整数提升的提升语义实现。
### 如何处理`uint64`?
混合有符号/无符号整数提升的方法中缺少一种类型:`uint64`。按照上述模式,涉及`uint64`的混合整数操作的输出应该是`int128`,但这不是标准可用的数据类型。
NumPy 在这里的选择是提升为`float64`:
“`py
(np.uint64(1) + np.int64(1)).dtype
dtype(\’float64\’)
然而,这可能是一个令人惊讶的约定:这是唯一一种整数类型提升不会产生整数的情况。目前,我们将保持uint64提升的未定义状态,并稍后再回到这个问题。
整数和浮点混合提升
当将整数提升为浮点数时,我们可能会从与有符号和无符号整数之间的混合提升相同的思路开始。16 位有符号或无符号整数无法被只有 10 位尾数的 16 位浮点数以全精度表示。因此,将整数提升为比特数加倍的浮点数可能是有道理的:
显示代码单元格源代码 隐藏代码单元格源代码
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’, \’f16\’], \’u16\’: [\’u32\’, \’i32\’, \’f32\’], \’u32\’: [\’u64\’, \’i64\’, \’f64\’],
\’i8\’: [\’i16\’, \’f16\’], \’i16\’: [\’i32\’, \’f32\’], \’i32\’: [\’i64\’, \’f64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [0.5, 2], \’f32\’: [1.5, 2], \’f64\’: [2.5, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 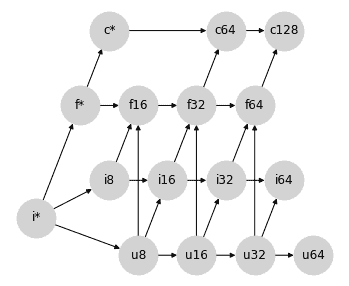
这实际上是 NumPy 类型提升所做的事情,但在这样做时它破坏了图的格性质:例如,对于*{i8, u8}*对,不再有唯一的最小上界:可能性有*i16*和*f16*,这在图上是不可排序的。这事实上是 NumPy 非可结合类型提升的根源。
我们能否提出 NumPy 提升规则的修改,以便满足格性质,并为混合类型提升提供明智的结果?我们在这里可以采取几种方法。
### 选项 0:将整数/浮点混合精度未定义
为了使行为完全可预测(虽然会损失用户方便性),一个可以辩护的选择是在 Python 标量之外将任何混合整数/浮点数提升保留为未定义状态,停留在前一节的部分格子结构。缺点是用户在操作整数和浮点数数量之间时需要显式类型转换。
### 选项 1:避免所有精度损失
如果我们的重点是以任何代价避免精度损失,我们可以通过其现有的有符号整数路径将无符号整数提升为浮点数来恢复格子属性:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源代码 隐藏代码单元格源代码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’],
\’i8\’: [\’i16\’, \’f16\’], \’i16\’: [\’i32\’, \’f32\’], \’i32\’: [\’i64\’, \’f64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [0.5, 2], \’f32\’: [1.5, 2], \’f64\’: [2.5, 2],
\’c64\’: [2, 3], \’c128\’: [3, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 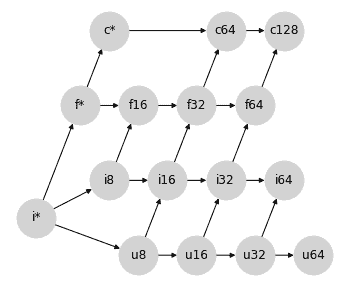
这种方法的一个缺点是它仍然使得`int64`和`uint64`的提升未定义,因为没有标准的浮点类型具有足够的尾数位来表示它们的完整值范围。我们可以放宽精度约束并通过从`i64->f64`和`u64->f64`的连接来完成格子,但这些连接会违反这种提升方案的动机。
第二个缺点是这种格子结构使得很难找到一个合理的位置来插入`bfloat16`(见下文),同时保持格子属性。
对于 JAX 加速器后端来说,这种方法的第三个缺点更为重要,即某些操作会导致比必要宽得多的类型;例如,`uint16` 和 `float16` 之间的混合操作会提升到`float64`,这并不理想。
### 选项 2:避免大部分比必要更宽的提升
为了解决更广泛类型的不必要提升,我们可以接受整数/浮点数提升可能会导致一些精度损失的可能性,将有符号整数提升为相同宽度的浮点数:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源代码 隐藏代码单元格源代码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’f*\’, \’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’f16\’, \’i32\’], \’i32\’: [\’f32\’, \’i64\’], \’i64\’: [\’f64\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [1.5, 2], \’f32\’: [2.5, 2], \’f64\’: [3.5, 2],
\’c64\’: [3, 3], \’c128\’: [4, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 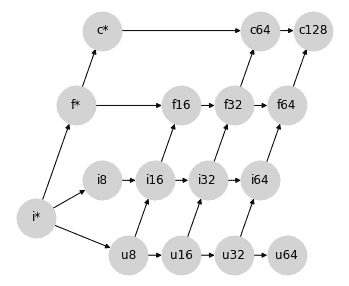
尽管这确实允许在整数和浮点数之间进行精度损失的提升,但这些提升不会误代表结果的*幅度*:虽然浮点数的尾数不足以表示所有值,但指数足以近似它们。
这种方法还允许从`int64`自然提升到`float64`,尽管在此方案中`uint64`仍然无法提升。也就是说,在这里更容易地可以通过其现有的有符号整数路径连接从`u64`到`f64`。
这种提升方案仍然会导致一些比必要更宽的提升路径;例如 `float32` 和 `uint32` 之间的操作将导致 `float64`。此外,这个格子使得很难找到一个合理的地方插入 `bfloat16`(见下文),同时保持格子属性。
### 选项 3:避免所有比必要更宽的提升
如果我们愿意从根本上改变我们对整数和浮点提升的思维方式,我们可以避免 *所有* 非理想的 64 位提升:就像标量总是遵循数组类型的宽度一样,我们可以使整数总是遵循浮点类型的宽度:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元源代码 隐藏代码单元源代码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’], \’i64\’: [\’f*\’],
\’f16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [1.5, 2], \’f32\’: [2.5, 2], \’f64\’: [3.5, 2],
\’c64\’: [3, 3], \’c128\’: [4, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 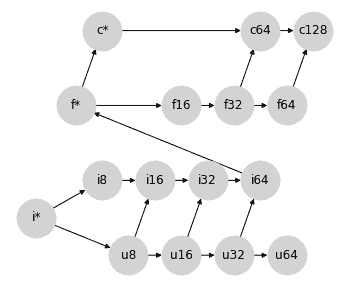
这涉及一种小的手法:之前我们使用 `f*` 表示标量类型。在这个格中,`f*` 可能被应用于混合计算的数组输出。我们不再将 `f*` 视为标量,而是可以将其视为一种具有不同提升规则的特殊类型 `float` 值:在 JAX 中我们称之为 *弱浮点数*;详见下文。
这种方法的优势在于,除了无符号整数外,它避免了 *所有* 比必要更宽的提升:你永远不会得到没有 64 位输入的 f64 输出,也永远不会得到没有 32 位输入的 f32 输出:这对于在加速器上工作时提供了方便的语义,同时避免了无意间生成 64 位值。
这种优先考虑浮点类型的特性类似于 PyTorch 的类型提升行为。这个格子也碰巧生成了一个非常接近 JAX 原始 *临时* 类型提升方案的提升表,该方案不是基于格子的,但具有优先考虑浮点类型的特性。
此外,这个格子还提供了一个自然的位置来插入 `bfloat16`,而无需在 `bf16` 和 `f16` 之间施加排序:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元源代码 隐藏代码单元源代码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’, \’bf16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’], \’i64\’: [\’f*\’],
\’f16\’: [\’f32\’], \’bf16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [-0.5, 2], \’c*\’: [0, 3],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [1.8, 1.7], \’bf16\’: [1.8, 2.3], \’f32\’: [3.0, 2], \’f64\’: [4.0, 2],
\’c64\’: [3.5, 3], \’c128\’: [4.5, 3],
}
fig, ax = plt.subplots(figsize=(6, 5))
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
“`</details> 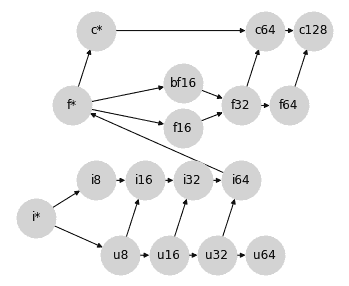
这一点很重要,因为 `f16` 和 `bf16` 不可比较,它们利用其位的方式不同:`bf16` 以较低精度表示更大的范围,而 `f16` 则以较高精度表示更小的范围。
然而,这些优势也伴随着一些权衡:
+ 混合浮点数/整数提升非常容易产生精度损失:例如,`int64`(最大值为 \\(9.2 \\times 10^{18}\\))可以提升为 `float16`(最大值为 \\(6.5 \\times 10⁴\\)),这意味着大多数可表示的值将变为 `inf`。
+ 如上所述,`f*`不再被视为“标量类型”,而是被视为 float64 的不同风味。在 JAX 术语中,这被称为[*弱类型*](https://jax.readthedocs.io/en/latest/type_promotion.html#weakly-typed-values-in-jax),即它表示为 64 位,但在与其他值推广时只弱化到此位宽度。
还请注意,这种方法仍然未解决`uint64`提升问题,尽管将`u64`连接到`f*`可能是合理的。
## JAX 中的类型提升
在设计 JAX 的类型提升语义时,我们牢记了许多这些想法,并且在几个方面倾向于:
1. 我们选择将 JAX 的类型提升语义约束为满足格属性的图形:这是为了确保结合律和交换律,但也为了允许语义被简洁地描述为 DAG,而不需要一个大表格。
1. 在计算加速器上获益时,我们倾向于避免意外推广到更宽的类型,特别是在涉及浮点值时。
1. 如果需要为了保持(1)和(2),我们可以接受在混合类型提升中潜在的精度损失(但不是幅度损失)。
考虑到这一点,JAX 采用了选项 3。或者更确切地说,选项 3 的一个稍微修改的版本,以建立`u64`与`f*`之间的连接,以创建真正的格。为了清晰起见重新排列节点,JAX 的类型提升格看起来像这样:
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源码 隐藏代码单元格源码</summary>
“`py
#@title
import networkx as nx
import matplotlib.pyplot as plt
lattice = {
\’i*\’: [\’u8\’, \’i8\’], \’f*\’: [\’c*\’, \’f16\’, \’bf16\’], \’c*\’: [\’c64\’],
\’u8\’: [\’u16\’, \’i16\’], \’u16\’: [\’u32\’, \’i32\’], \’u32\’: [\’u64\’, \’i64\’], \’u64\’: [\’f*\’],
\’i8\’: [\’i16\’], \’i16\’: [\’i32\’], \’i32\’: [\’i64\’], \’i64\’: [\’f*\’],
\’f16\’: [\’f32\’], \’bf16\’: [\’f32\’], \’f32\’: [\’f64\’, \’c64\’], \’f64\’: [\’c128\’],
\’c64\’: [\’c128\’]
}
graph = nx.from_dict_of_lists(lattice, create_using=nx.DiGraph)
pos = {
\’i*\’: [-1.25, 0.5], \’f*\’: [4.5, 0.5], \’c*\’: [5, 1.5],
\’u8\’: [0.5, 0], \’u16\’: [1.5, 0], \’u32\’: [2.5, 0], \’u64\’: [3.5, 0],
\’i8\’: [0, 1], \’i16\’: [1, 1], \’i32\’: [2, 1], \’i64\’: [3, 1],
\’f16\’: [5.75, 0.8], \’bf16\’: [5.75, 0.2], \’f32\’: [7, 0.5], \’f64\’: [8, 0.5],
\’c64\’: [7.5, 1.5], \’c128\’: [8.5, 1.5],
}
fig, ax = plt.subplots(figsize=(10, 4))
ax.set_ylim(-0.5, 2)
nx.draw(graph, with_labels=True, node_size=1500, node_color=\’lightgray\’, pos=pos, ax=ax)
# ax.patches[12].set_linestyle((0, (2, 4)))
“`</details> 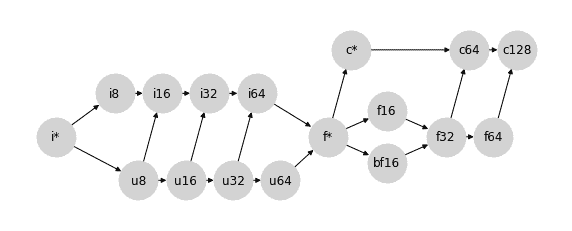
从这种选择产生的行为总结在[JAX 类型提升语义](https://jax.readthedocs.io/en/latest/type_promotion.html)中。特别地,除了包括更大的无符号类型(`u16`、`u32`、`u64`)和一些关于标量/弱类型(`i*`、`f*`、`c*`)行为的细节外,这种类型提升方案与 PyTorch 选择的非常接近。
对于有兴趣的人,附录下面打印了 NumPy、Tensorflow、PyTorch 和 JAX 使用的完整推广表。
## 附录:示例类型提升表
下面是各种 Python 数组计算库实现的隐式类型提升表的一些示例。
### NumPy 类型提升
请注意,NumPy 不包括`bfloat16` dtype,并且下表忽略了依赖值影响。
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源码 隐藏代码单元格源码</summary>
“`py
# @title
import numpy as np
import pandas as pd
from IPython import display
np_dtypes = {
\’b\’: np.bool_,
\’u8\’: np.uint8, \’u16\’: np.uint16, \’u32\’: np.uint32, \’u64\’: np.uint64,
\’i8\’: np.int8, \’i16\’: np.int16, \’i32\’: np.int32, \’i64\’: np.int64,
\’bf16\’: \’invalid\’, \’f16\’: np.float16, \’f32\’: np.float32, \’f64\’: np.float64,
\’c64\’: np.complex64, \’c128\’: np.complex128,
\’i*\’: int, \’f*\’: float, \’c*\’: complex}
np_dtype_to_code = {val: key for key, val in np_dtypes.items()}
def make_np_zero(dtype):
if dtype in {int, float, complex}:
return dtype(0)
else:
return np.zeros(1, dtype=dtype)
def np_result_code(dtype1, dtype2):
try:
out = np.add(make_np_zero(dtype1), make_np_zero(dtype2))
except TypeError:
return \’-\’
else:
if type(out) in {int, float, complex}:
return np_dtype_to_code[type(out)]
else:
return np_dtype_to_code[out.dtype.type]
grid = [[np_result_code(dtype1, dtype2)
for dtype2 in np_dtypes.values()]
for dtype1 in np_dtypes.values()]
table = pd.DataFrame(grid, index=np_dtypes.keys(), columns=np_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | – | f16 | f32 | f64 | c64 | c128 | i64 | f64 | c128 |
| u8 | u8 | u8 | u16 | u32 | u64 | i16 | i16 | i32 | i64 | – | f16 | f32 | f64 | c64 | c128 | u8 | f64 | c128 |
| u16 | u16 | u16 | u16 | u32 | u64 | i32 | i32 | i32 | i64 | – | f32 | f32 | f64 | c64 | c128 | u16 | f64 | c128 |
| u32 | u32 | u32 | u32 | u32 | u64 | i64 | i64 | i64 | i64 | – | f64 | f64 | f64 | c128 | c128 | u32 | f64 | c128 |
| u64 | u64 | u64 | u64 | u64 | u64 | f64 | f64 | f64 | f64 | – | f64 | f64 | f64 | c128 | c128 | u64 | f64 | c128 |
| i8 | i8 | i16 | i32 | i64 | f64 | i8 | i16 | i32 | i64 | – | f16 | f32 | f64 | c64 | c128 | i8 | f64 | c128 |
| i16 | i16 | i16 | i32 | i64 | f64 | i16 | i16 | i32 | i64 | – | f32 | f32 | f64 | c64 | c128 | i16 | f64 | c128 |
| i32 | i32 | i32 | i32 | i64 | f64 | i32 | i32 | i32 | i64 | – | f64 | f64 | f64 | c128 | c128 | i32 | f64 | c128 |
| i64 | i64 | i64 | i64 | i64 | f64 | i64 | i64 | i64 | i64 | – | f64 | f64 | f64 | c128 | c128 | i64 | f64 | c128 |
| bf16 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| f16 | f16 | f16 | f32 | f64 | f64 | f16 | f32 | f64 | f64 | – | f16 | f32 | f64 | c64 | c128 | f16 | f16 | c64 |
| f32 | f32 | f32 | f32 | f64 | f64 | f32 | f32 | f64 | f64 | – | f32 | f32 | f64 | c64 | c128 | f32 | f32 | c64 |
| f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | – | f64 | f64 | f64 | c128 | c128 | f64 | f64 | c128 |
| c64 | c64 | c64 | c64 | c128 | c128 | c64 | c64 | c128 | c128 | – | c64 | c64 | c128 | c64 | c128 | c64 | c64 | c64 |
| c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | – | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 |
| i* | i64 | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | – | f16 | f32 | f64 | c64 | c128 | i64 | f64 | c128 |
| f* | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | – | f16 | f32 | f64 | c64 | c128 | f64 | f64 | c128 |
| c* | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | – | c64 | c64 | c128 | c64 | c128 | c128 | c128 | c128 |
### TensorFlow 类型提升
TensorFlow 避免定义隐式类型提升,除了在有限的情况下,对 Python 标量进行操作。该表格是不对称的,因为在 `tf.add(x, y)` 中,`y` 的类型必须可以强制转换为 `x` 的类型。
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格来源 隐藏代码单元格来源</summary>
“`py
# @title
import tensorflow as tf
import pandas as pd
from IPython import display
tf_dtypes = {
\’b\’: tf.bool,
\’u8\’: tf.uint8, \’u16\’: tf.uint16, \’u32\’: tf.uint32, \’u64\’: tf.uint64,
\’i8\’: tf.int8, \’i16\’: tf.int16, \’i32\’: tf.int32, \’i64\’: tf.int64,
\’bf16\’: tf.bfloat16, \’f16\’: tf.float16, \’f32\’: tf.float32, \’f64\’: tf.float64,
\’c64\’: tf.complex64, \’c128\’: tf.complex128,
\’i*\’: int, \’f*\’: float, \’c*\’: complex}
tf_dtype_to_code = {val: key for key, val in tf_dtypes.items()}
def make_tf_zero(dtype):
if dtype in {int, float, complex}:
return dtype(0)
else:
return tf.zeros(1, dtype=dtype)
def result_code(dtype1, dtype2):
try:
out = tf.add(make_tf_zero(dtype1), make_tf_zero(dtype2))
except (TypeError, tf.errors.InvalidArgumentError):
return \’-\’
else:
if type(out) in {int, float, complex}:
return tf_dtype_to_code[type(out)]
else:
return tf_dtype_to_code[out.dtype]
grid = [[result_code(dtype1, dtype2)
for dtype2 in tf_dtypes.values()]
for dtype1 in tf_dtypes.values()]
table = pd.DataFrame(grid, index=tf_dtypes.keys(), columns=tf_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u8 | – | u8 | – | – | – | – | – | – | – | – | – | – | – | – | – | u8 | – | – |
| u16 | – | – | u16 | – | – | – | – | – | – | – | – | – | – | – | – | u16 | – | – |
| u32 | – | – | – | u32 | – | – | – | – | – | – | – | – | – | – | – | u32 | – | – |
| u64 | – | – | – | – | u64 | – | – | – | – | – | – | – | – | – | – | u64 | – | – |
| i8 | – | – | – | – | – | i8 | – | – | – | – | – | – | – | – | – | i8 | – | – |
| i16 | – | – | – | – | – | – | i16 | – | – | – | – | – | – | – | – | i16 | – | – |
| i32 | – | – | – | – | – | – | – | i32 | – | – | – | – | – | – | – | i32 | – | – |
| i64 | – | – | – | – | – | – | – | – | i64 | – | – | – | – | – | – | i64 | – | – |
| bf16 | – | – | – | – | – | – | – | – | – | bf16 | – | – | – | – | – | bf16 | bf16 | – |
| f16 | – | – | – | – | – | – | – | – | – | – | f16 | – | – | – | – | f16 | f16 | – |
| f32 | – | – | – | – | – | – | – | – | – | – | – | f32 | – | – | – | f32 | f32 | – |
| f64 | – | – | – | – | – | – | – | – | – | – | – | – | f64 | – | – | f64 | f64 | – |
| c64 | – | – | – | – | – | – | – | – | – | – | – | – | – | c64 | – | c64 | c64 | c64 |
| c128 | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | c128 | c128 | c128 |
| i* | – | – | – | – | – | – | – | i32 | – | – | – | – | – | – | – | i32 | – | – |
| f* | – | – | – | – | – | – | – | – | – | – | – | f32 | – | – | – | f32 | f32 | – |
| c* | – | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | c128 | c128 | c128 |
### PyTorch 类型提升
注意,torch 不包括大于 `uint8` 的无符号整数类型。除此之外,有关标量/弱类型提升的一些细节,表格接近于 `jax.numpy` 的用法。
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元源代码 隐藏代码单元源代码</summary>
“`py
# @title
import torch
import pandas as pd
from IPython import display
torch_dtypes = {
\’b\’: torch.bool,
\’u8\’: torch.uint8, \’u16\’: \’invalid\’, \’u32\’: \’invalid\’, \’u64\’: \’invalid\’,
\’i8\’: torch.int8, \’i16\’: torch.int16, \’i32\’: torch.int32, \’i64\’: torch.int64,
\’bf16\’: torch.bfloat16, \’f16\’: torch.float16, \’f32\’: torch.float32, \’f64\’: torch.float64,
\’c64\’: torch.complex64, \’c128\’: torch.complex128,
\’i*\’: int, \’f*\’: float, \’c*\’: complex}
torch_dtype_to_code = {val: key for key, val in torch_dtypes.items()}
def make_torch_zero(dtype):
if dtype in {int, float, complex}:
return dtype(0)
else:
return torch.zeros(1, dtype=dtype)
def torch_result_code(dtype1, dtype2):
try:
out = torch.add(make_torch_zero(dtype1), make_torch_zero(dtype2))
except TypeError:
return \’-\’
else:
if type(out) in {int, float, complex}:
return torch_dtype_to_code[type(out)]
else:
return torch_dtype_to_code[out.dtype]
grid = [[torch_result_code(dtype1, dtype2)
for dtype2 in torch_dtypes.values()]
for dtype1 in torch_dtypes.values()]
table = pd.DataFrame(grid, index=torch_dtypes.keys(), columns=torch_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | b | u8 | – | – | – | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i64 | f32 | c64 |
| u8 | u8 | u8 | – | – | – | i16 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | u8 | f32 | c64 |
| u16 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u32 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u64 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| i8 | i8 | i16 | – | – | – | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i8 | f32 | c64 |
| i16 | i16 | i16 | – | – | – | i16 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i16 | f32 | c64 |
| i32 | i32 | i32 | – | – | – | i32 | i32 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i32 | f32 | c64 |
| i64 | i64 | i64 | – | – | – | i64 | i64 | i64 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i64 | f32 | c64 |
| bf16 | bf16 | bf16 | – | – | – | bf16 | bf16 | bf16 | bf16 | bf16 | f32 | f32 | f64 | c64 | c128 | bf16 | bf16 | c64 |
| f16 | f16 | f16 | – | – | – | f16 | f16 | f16 | f16 | f32 | f16 | f32 | f64 | c64 | c128 | f16 | f16 | c64 |
| f32 | f32 | f32 | – | – | – | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f64 | c64 | c128 | f32 | f32 | c64 |
| f64 | f64 | f64 | – | – | – | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | c128 | c128 | f64 | f64 | c128 |
| c64 | c64 | c64 | – | – | – | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c128 | c64 | c128 | c64 | c64 | c64 |
| c128 | c128 | c128 | – | – | – | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 |
| i* | i64 | u8 | – | – | – | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i64 | f32 | c64 |
| f* | f32 | f32 | – | – | – | f32 | f32 | f32 | f32 | bf16 | f16 | f32 | f64 | c64 | c128 | f32 | f64 | c64 |
| c* | c64 | c64 | – | – | – | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c128 | c64 | c128 | c64 | c64 | c128 |
### JAX Type Promotion: `jax.numpy`
`jax.numpy` follows type promotion rules laid out at https://jax.readthedocs.io/en/latest/type_promotion.html. Here we use `i*`, `f*`, `c*` to indicate both Python scalars and weakly-typed arrays.
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源码 隐藏代码单元格源码</summary>
“`py
# @title
from jax import dtypes
import jax
import jax.numpy as jnp
import pandas as pd
from IPython import display
jax.config.update(\’jax_enable_x64\’, True)
jnp_dtypes = {
\’b\’: jnp.bool_.dtype,
\’u8\’: jnp.uint8.dtype, \’u16\’: jnp.uint16.dtype, \’u32\’: jnp.uint32.dtype, \’u64\’: jnp.uint64.dtype,
\’i8\’: jnp.int8.dtype, \’i16\’: jnp.int16.dtype, \’i32\’: jnp.int32.dtype, \’i64\’: jnp.int64.dtype,
\’bf16\’: jnp.bfloat16.dtype, \’f16\’: jnp.float16.dtype, \’f32\’: jnp.float32.dtype, \’f64\’: jnp.float64.dtype,
\’c64\’: jnp.complex64.dtype, \’c128\’: jnp.complex128.dtype,
\’i*\’: int, \’f*\’: float, \’c*\’: complex}
jnp_dtype_to_code = {val: key for key, val in jnp_dtypes.items()}
def make_jnp_zero(dtype):
if dtype in {int, float, complex}:
return dtype(0)
else:
return jnp.zeros((), dtype=dtype)
def jnp_result_code(dtype1, dtype2):
try:
out = jnp.add(make_jnp_zero(dtype1), make_jnp_zero(dtype2))
except TypeError:
return \’-\’
else:
if hasattr(out, \’aval\’) and out.aval.weak_type:
return out.dtype.kind + \’*\’
elif type(out) in {int, float, complex}:
return jnp_dtype_to_code[type(out)]
else:
return jnp_dtype_to_code[out.dtype]
grid = [[jnp_result_code(dtype1, dtype2)
for dtype2 in jnp_dtypes.values()]
for dtype1 in jnp_dtypes.values()]
table = pd.DataFrame(grid, index=jnp_dtypes.keys(), columns=jnp_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| u8 | u8 | u8 | u16 | u32 | u64 | i16 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | u8 | f* | c* |
| u16 | u16 | u16 | u16 | u32 | u64 | i32 | i32 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | u16 | f* | c* |
| u32 | u32 | u32 | u32 | u32 | u64 | i64 | i64 | i64 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | u32 | f* | c* |
| u64 | u64 | u64 | u64 | u64 | u64 | f* | f* | f* | f* | bf16 | f16 | f32 | f64 | c64 | c128 | u64 | f* | c* |
| i8 | i8 | i16 | i32 | i64 | f* | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i8 | f* | c* |
| i16 | i16 | i16 | i32 | i64 | f* | i16 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i16 | f* | c* |
| i32 | i32 | i32 | i32 | i64 | f* | i32 | i32 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i32 | f* | c* |
| i64 | i64 | i64 | i64 | i64 | f* | i64 | i64 | i64 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i64 | f* | c* |
| bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | bf16 | f32 | f32 | f64 | c64 | c128 | bf16 | bf16 | c64 |
| f16 | f16 | f16 | f16 | f16 | f16 | f16 | f16 | f16 | f16 | f32 | f16 | f32 | f64 | c64 | c128 | f16 | f16 | c64 |
| f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f32 | f64 | c64 | c128 | f32 | f32 | c64 |
| f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | f64 | c128 | c128 | f64 | f64 | c128 |
| c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c64 | c128 | c64 | c128 | c64 | c64 | c64 |
| c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 | c128 |
| i* | i* | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| f* | f* | f* | f* | f* | f* | f* | f* | f* | f* | bf16 | f16 | f32 | f64 | c64 | c128 | f* | f* | c* |
| c* | c* | c* | c* | c* | c* | c* | c* | c* | c* | c64 | c64 | c64 | c128 | c64 | c128 | c* | c* | c* |
### JAX 类型提升:`jax.lax`
`jax.lax` 是较低级的库,不执行任何隐式类型提升。在这里,我们使用 `i*`、`f*`、`c*` 来表示 Python 标量和弱类型数组。
<details class=\”hide above-input\”><summary aria-label=\”Toggle hidden content\”>显示代码单元格源代码 隐藏代码单元格源代码</summary>
“`py
# @title
from jax import dtypes
import jax
import jax.numpy as jnp
import pandas as pd
from IPython import display
jax.config.update(\’jax_enable_x64\’, True)
jnp_dtypes = {
\’b\’: jnp.bool_.dtype,
\’u8\’: jnp.uint8.dtype, \’u16\’: jnp.uint16.dtype, \’u32\’: jnp.uint32.dtype, \’u64\’: jnp.uint64.dtype,
\’i8\’: jnp.int8.dtype, \’i16\’: jnp.int16.dtype, \’i32\’: jnp.int32.dtype, \’i64\’: jnp.int64.dtype,
\’bf16\’: jnp.bfloat16.dtype, \’f16\’: jnp.float16.dtype, \’f32\’: jnp.float32.dtype, \’f64\’: jnp.float64.dtype,
\’c64\’: jnp.complex64.dtype, \’c128\’: jnp.complex128.dtype,
\’i*\’: int, \’f*\’: float, \’c*\’: complex}
jnp_dtype_to_code = {val: key for key, val in jnp_dtypes.items()}
def make_jnp_zero(dtype):
if dtype in {int, float, complex}:
return dtype(0)
else:
return jnp.zeros((), dtype=dtype)
def jnp_result_code(dtype1, dtype2):
try:
out = jax.lax.add(make_jnp_zero(dtype1), make_jnp_zero(dtype2))
except TypeError:
return \’-\’
else:
if hasattr(out, \’aval\’) and out.aval.weak_type:
return out.dtype.kind + \’*\’
elif type(out) in {int, float, complex}:
return jnp_dtype_to_code[type(out)]
else:
return jnp_dtype_to_code[out.dtype]
grid = [[jnp_result_code(dtype1, dtype2)
for dtype2 in jnp_dtypes.values()]
for dtype1 in jnp_dtypes.values()]
table = pd.DataFrame(grid, index=jnp_dtypes.keys(), columns=jnp_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u8 | – | u8 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u16 | – | – | u16 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u32 | – | – | – | u32 | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u64 | – | – | – | – | u64 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| i8 | – | – | – | – | – | i8 | – | – | – | – | – | – | – | – | – | – | – | – |
| i16 | – | – | – | – | – | – | i16 | – | – | – | – | – | – | – | – | – | – | – |
| i32 | – | – | – | – | – | – | – | i32 | – | – | – | – | – | – | – | – | – | – |
| i64 | – | – | – | – | – | – | – | – | i64 | – | – | – | – | – | – | i64 | – | – |
| bf16 | – | – | – | – | – | – | – | – | – | bf16 | – | – | – | – | – | – | – | – |
| f16 | – | – | – | – | – | – | – | – | – | – | f16 | – | – | – | – | – | – | – |
| f32 | – | – | – | – | – | – | – | – | – | – | – | f32 | – | – | – | – | – | – |
| f64 | – | – | – | – | – | – | – | – | – | – | – | – | f64 | – | – | – | f64 | – |
| c64 | – | – | – | – | – | – | – | – | – | – | – | – | – | c64 | – | – | – | – |
| c128 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | – | – | c128 |
| i* | – | – | – | – | – | – | – | – | i64 | – | – | – | – | – | – | i* | – | – |
| f* | – | – | – | – | – | – | – | – | – | – | – | – | f64 | – | – | – | f* | – |
| c* | – | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | – | – | c* |
return \’-\’
else:
if hasattr(out, \’aval\’) and out.aval.weak_type:
return out.dtype.kind + \’*\’
elif type(out) in {int, float, complex}:
return jnp_dtype_to_code[type(out)]
else:
return jnp_dtype_to_code[out.dtype]
grid = [[jnp_result_code(dtype1, dtype2)
for dtype2 in jnp_dtypes.values()]
for dtype1 in jnp_dtypes.values()]
table = pd.DataFrame(grid, index=jnp_dtypes.keys(), columns=jnp_dtypes.keys())
display.HTML(table.to_html())
“`</details>
| | b | u8 | u16 | u32 | u64 | i8 | i16 | i32 | i64 | bf16 | f16 | f32 | f64 | c64 | c128 | i* | f* | c* |
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| b | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u8 | – | u8 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u16 | – | – | u16 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u32 | – | – | – | u32 | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| u64 | – | – | – | – | u64 | – | – | – | – | – | – | – | – | – | – | – | – | – |
| i8 | – | – | – | – | – | i8 | – | – | – | – | – | – | – | – | – | – | – | – |
| i16 | – | – | – | – | – | – | i16 | – | – | – | – | – | – | – | – | – | – | – |
| i32 | – | – | – | – | – | – | – | i32 | – | – | – | – | – | – | – | – | – | – |
| i64 | – | – | – | – | – | – | – | – | i64 | – | – | – | – | – | – | i64 | – | – |
| bf16 | – | – | – | – | – | – | – | – | – | bf16 | – | – | – | – | – | – | – | – |
| f16 | – | – | – | – | – | – | – | – | – | – | f16 | – | – | – | – | – | – | – |
| f32 | – | – | – | – | – | – | – | – | – | – | – | f32 | – | – | – | – | – | – |
| f64 | – | – | – | – | – | – | – | – | – | – | – | – | f64 | – | – | – | f64 | – |
| c64 | – | – | – | – | – | – | – | – | – | – | – | – | – | c64 | – | – | – | – |
| c128 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | – | – | c128 |
| i* | – | – | – | – | – | – | – | – | i64 | – | – | – | – | – | – | i* | – | – |
| f* | – | – | – | – | – | – | – | – | – | – | – | – | f64 | – | – | – | f* | – |
| c* | – | – | – | – | – | – | – | – | – | – | – | – | – | – | c128 | – | – | c* |
#以上关于JAX 中文文档(十一)的相关内容来源网络仅供参考,相关信息请以官方公告为准!
原创文章,作者:CSDN,如若转载,请注明出处:https://www.sudun.com/ask/91407.html

